Z-Test vs T-Test

Last Updated :

Blog Author :

Edited by :

Reviewed by :

Table Of Contents

Differences Between Z-Test and T-Test

Z-test is the statistical hypothesis used to determine whether the two samples' means calculated are different if the standard deviation is available and the sample is large. In contrast, the T-test determines how averages of different data sets differ in case the standard deviation or the variance is unknown.

Z-tests and T-tests are the two statistical methods that involve data analysis, which has applications in science, business, and many other disciplines. The T-test is a univariate hypothesis test based on T-statistics, wherein the mean, i.e., the average, is known, and population variance, i.e., the standard deviation, is approximated from the sample. On the other hand, Z-test is also a univariate test based on a standard normal distribution.

Differences Between Z-Test and T-Test

Uses

#1 - Z-Test

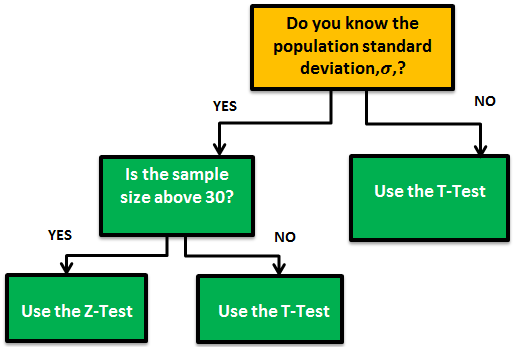
Z-test Formula, as mentioned earlier, are the statistical calculations that one can use to compare population averages to a sample's. The Z-test will tell you how far, in standard deviations terms, a data point is from the average of a data set. A Z-test will compare a sample to a defined population one typically uses for dealing with problems relating to large samples (i.e., n > 30). Mostly, they are very useful when the standard deviation is known.

#2 - T-Test

T-tests are also calculations one can use to test a hypothesis. Still, they are very useful when determining if there is a statistically significant comparison between the two independent sample groups. In other words, a t-test asks whether the comparison between the averages of 2 groups is unlikely to have occurred due to random chance. Usually, T-tests are more appropriate when dealing with problems with a limited sample size (i.e., n < 30).

Z-Test vs. T-Test Infographics

Here we provide you with the top 5 differences between the z-test vs. t-test you must know.

Key Differences

One of the essential conditions for conducting a T-test is that the population standard deviation or the variance is unknown. Conversely, the population variance formula, should be assumed to be known or known in the case of a Z-test.
The t-test, as mentioned earlier, is based on student's t-distribution. On the contrary, the Z-test assumes that the distribution of sample means will be normal. The normal distribution and the student's T- distribution appear the same, as both are bell-shaped and symmetrical. However, they differ in one of the cases with less space in the center and more in their tails in T-distribution.
Z-test is used as given in the above table when the sample size is large, which is n > 30, and the t-test is appropriate when the sample size is not big, which is small, i.e., that n < 30.

Z-Test vs. T-Test Comparative Table

Basis	Z Test	T-Test
Basic Definition	Z-test is a kind of hypothesis test which ascertains if the averages of the 2 datasets are different from each other when standard deviation or variance is given.	The t-test can be referred to as a kind of parametric test that is applied to an identity, how the averages of 2 sets of data differ from each other when the standard deviation or variance is not given.
Population Variance	The Population variance or standard deviation is known here.	The Population variance or standard deviation is unknown here.
Sample Size	The Sample size is large.	Here the Sample Size is small.
Key Assumptions	All data points are independent. Normal Distribution for Z, with an average zero and variance = 1.	All data points are not dependent. Sample values are to be recorded and taken accurately.
Based upon (a type of distribution)	Based on Normal distribution.	Based on Student-t distribution.

Conclusion

By and to a larger extent, these tests are almost similar. Still, the comparison comes only to their conditions for their application, meaning that the T-test is more appropriate and applicable when the sample size is not more than thirty units. However, if it is greater than thirty units, one should use a Z-test. Similarly, other conditions will clarify which test to perform in a situation.

There are also different tests like the F-test, two-tailed vs. single-tailed, etc., so statisticians must be careful after analyzing the situation and then deciding which one to use. Below is a sample chart for what we discussed above.