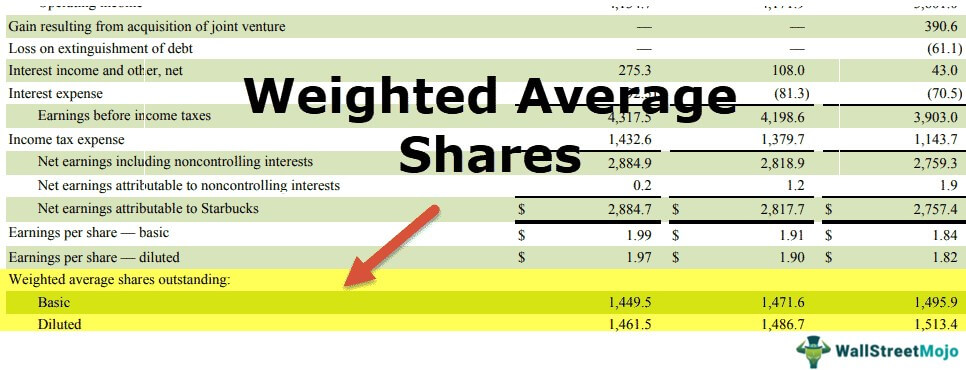
Weighted Average Shares Outstanding

The weighted average share outstanding is calculated by multiplying an outstanding number of shares after considering issuance and buybacks of shares in each reporting period with its time-weighted portion and after that, summing up the total for each reporting period in a fiscal year.

What are Weighted Average Shares Outstanding?

Weighted average shares outstanding is the number of company shares after incorporating changes in the shares during the year. The number of company shares can vary during the year for various reasons. E.g., buyback of shares, the new issue of shares, share dividend, stock split, conversion of warrants, etc. Thus, while calculating Earnings per Share, the Company needs to find the weighted average number of shares outstanding. It incorporates all such scenarios of changes in the weighted average number of shares to give fair Earnings per share value.

Steps to Calculate Weighted Average Shares Outstanding

The following are the three steps to calculate weighted average shares outstanding.

1. The first step is to find the common shares count at the beginning of the year and the changes in common shares during the year.
2. Calculate the updated common shares after each change.
   • The issuance of new shares increases the common share count.
   • The repurchase of shares reduces the common share count.
3. Weight the shares outstanding by the portion of the year between this change and the next change: weight = days outstanding / 365 = months outstanding / 12

Weighted Average Shares Outstanding Explained in Video

Weighted Average Shares Outstanding Calculation

Let us consider the following example and incorporate various scenarios that can affect the weighted average number of shares outstanding.

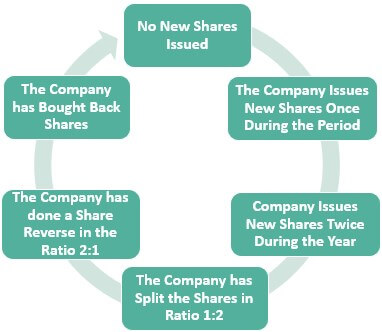
#1 - No New Shares Issued

Let there be a Company A that has 100 thousand shares outstanding at the start of the year, i.e., 1 January. The Company did not issue any new shares.

• Thus, weighted average shares outstanding = (100000 X 12)/ 12 = 100000

We multiplied the number by 12 for each month and did an average over these 12 months. Since no new shares were issued in this case, each month had 100 thousand shares outstanding; hence, the Company had 1 thousand shares outstanding over the year.

#2 - The Company Issues New Shares Once During the Period

Now, Company A issued 12 thousand new shares on 1 April.

• Thus, the Company had 100 thousand shares for the first three months and 112000 shares for the rest of the nine months.
• Thus, weighted average shares outstanding in this case = (100000*3 + 112000*9)/12 = 1308000/12 = 109000
• Thus, the weighted average shares outstanding in this case, the Company has 109,000 shares outstanding at the end of the year.

We pro-rated the weighted average number of shares according to their duration. Simply put, the funds generated from issuing new shares were available to the Company for nine months only; hence, these numbers were pro-rated.

#3 - Company Issues New Shares Twice During the Year

Company A issued another 12 thousand shares on 1 October during the year. Let us see how the weighted average number of shares outstanding will change.

• Thus, the Company has 100 thousand shares during the first three months, 112000 shares during the next six months, and 124000 shares during the last three months.
• Thus, weighted average shares outstanding in this case = (100000*3 + 112000*6 + 124000*3)/12 = 1344000/12 = 112000
• Thus, the weighted average shares outstanding in this case, the Company has 112,000 shares outstanding at the end of the year.
• Hence, from this example, we can say whenever there is a new issuance of shares, we will add them to the existing number of shares and prorate during the part of the year they were available for the Company.

However, the case changes whenever the Company does a stock split or a share reverse.

First, let us consider the Company has done a stock split.

#4 - The Company has Split the Shares in Ratio 1:2

From the above scenario, the Company split shares in the ratio of 1:2, i.e., an investor received one additional share for each.

Let Company A split the shares on 1^st December.

• In such a case, all the previous shares in the Company are multiplied by 2. This is because the value of the shares is the same before and after the stock split. The investor does not lose or gain from such measures.
• Hence, the weighted average number of shares will be = (200000*3 + 224000*6 + 248000*3)/12 = 2688000/12 = 224000
• Thus, the weighted average number of shares outstanding has also doubled by doing a stock split.

Now, let us consider the scenario of a share reverse. A share reverse is nothing but the opposite of the stock split. If the investor holds two shares in the Company, he will now have one share.

#5 - The Company has done a Share Reverse in the Ratio 2:1

From the above scenario, the Company did a share reverse in the ratio of 2:1, i.e., an investor will now have one share for every two shares held in the Company.

Let Company A do a share reverse on 1^st December.

• Now, in such a case, all the previous shares in the Company are divided by 2.
• Hence, the weighted average number of shares will be = (50000*3 + 56000*6 + 62000*3)/12 = 672000/12 = 56000
• Clearly, after the shared reverse, the number of outstanding shares has halved.

#6 - The Company has Bought Back Shares

We have seen corporate actions above and their treatment of the weighted average outstanding shares. Now, let us look into the buyback of shares. If the Company buys back the shares, they are treated similarly to the shares issued, but on the opposite, the shares are reduced from the calculation.

From scenario 3, Company A buys back 12000 shares on 1 October.

• Thus, the Company has 100 thousand shares during the first three months, 112000 shares during the next six months, and 100000 shares again during the last three months.
• Thus, weighted average shares outstanding in this case = (100000*3 + 112000*6 + 100000*3)/12 = 1272000/12 = 106000
• Thus, the Company has 106,000 shares outstanding at the end of the year.

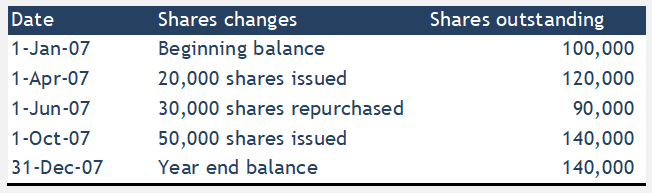
Weighted Average Share Calculation Example #1

Below is the Weighted Average Shares calculation example when shares are issued and repurchased during the year.

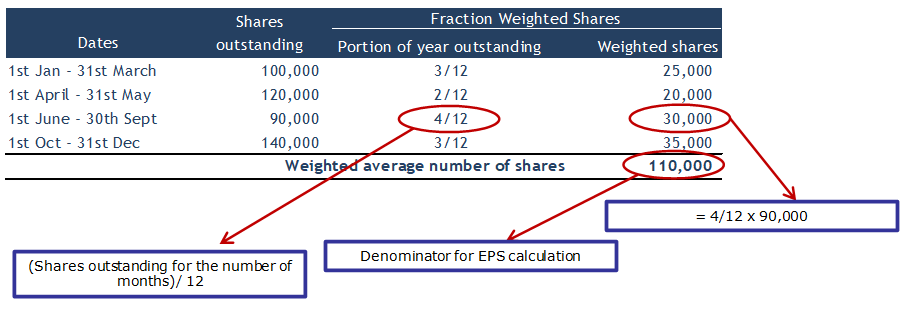
The below table shows the weighted averages shares outstanding calculation in a tabular format.

Weighted Average Share Outstanding Calculation Example #2

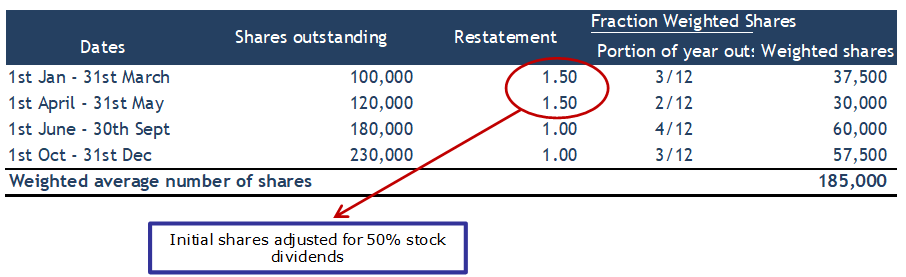
This second example of weighted average shares outstanding calculation considers the cases when shares are issued and stock dividends are given during the year.

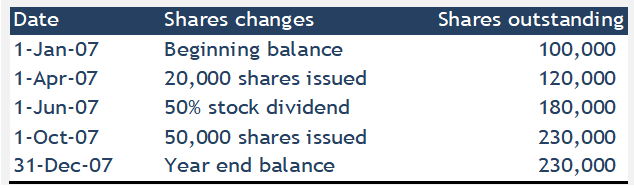
The below table shows the weighted averages shares outstanding calculation in a tabular format.

Conclusion

Weighted average outstanding shares are an important factor during the calculation of earnings per share for the Company. Since the number of shares of the Company keeps changing due to various corporate actions like-new issue of shares, buyback of shares, stock split, stock reverse, etc. and the new shares or the shares bought back were available with the Company for a proportion of the year, it makes sense to prorate the shares to find a weighted average.

Recommended Articles

This has been a guide to what weighted average shares outstanding. Here we look at the steps to calculate it in shares issuance, repurchase, stock dividends, stock splits, share reverse, and more. You may have a look at these articles below to learn more about accounting –

• Reverse Stock Split Definition
• Shared issued Types
• What is a Stock Dividend?
• Earnings Per Share Formula
• Preferred Stock