Variance

Publication Date :

Blog Author :

Edited by :

Reviewed by :

Table Of Contents

arrow

Variance Meaning

Variance is a statistical method used to calculate the expected deviation between values in a dataset. The main objective of this method is to determine the overall spread or variability among the variables.

Variance Meaning

Variance plays a crucial role in statistical analysis and experimentation. It considers each variable in the dataset and measures the distance of each variable from the mean. It is an important parameter in research because it provides insight into the variability of the data. However, unequal values in the dataset can lead to biased results.

Table of contents
  • Variance is a statistical parameter businesses and researchers use to calculate the deviation of the actual value (or data point) from the average (mean).
  • The concept of this method has existed since the 18th century, and several mathematicians, including Carl Friedrich Gauss, introduced it. Later, in 1918, Sir Ronald Aylmer Fisher gave the theory in a paper.
  • A low value indicates that many data points are gathered around the mean, while a high value signals that the points are spread far apart from the mean.
  • Standard deviation is the square root of variance. Although both are related, these methods have different purposes.

Variance Explained

Variance is a statistical measure used to calculate the spread or distance between numbers in a dataset. It helps to understand the relationship between individual numbers. It is often used with other measures, such as standard deviation and covariance, to understand the data fully. The history of variance dates back to the 18th century when the German mathematician Carl Friedrich Gauss studied the distribution of the stars. Later, in 1918, Sir Ronald Aylmer Fisher introduced the concept of variance in a paper. 

Variance is a statistical measure that enables a person to gauge the variability between actual and expected values. In other words, it determines how far each number in a dataset is from the mean. The data is more scattered or spread apart if the variance is high. Conversely, if it is low, the data points are more tightly clustered around the mean. A low value indicates less deviation from the mean. Thus, businesses can use it in statistics to evaluate the consistency of their data. If data values fluctuate significantly over time, the variance will be higher, indicating greater variability.

Researchers use raw data and scores to calculate variance in statistics. In addition to researchers, traders can use it to assess a company's financial performance. Furthermore, businesses can use it to measure the spread of expenses from the actual budget with consistent sample size. Since variance deals with the average spread of the data, it can be used to compare groups with different sample sizes. However, variance is slightly different from standard deviation, which measures the degree of dispersion from the mean rather than the average spread.

While both variance and standard deviation measure the spread of a dataset, the standard deviation is the square root of the variance and is dependent on it. The main disadvantage of using both measures is that they can yield different values for the same dataset. It is because variance is calculated by taking the average of the squared differences from the mean, while standard deviation is calculated by taking the square root of the variance. As a result, they have different units of measurement and may produce different results, even though they both aim to provide insight into the spread of the data.

Formula

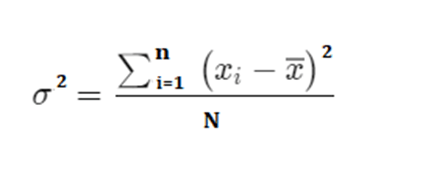
Variance Formula
Where,

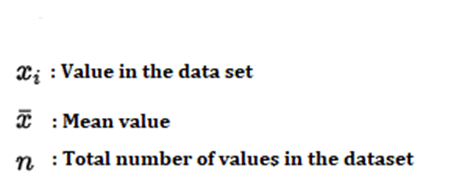
Calculation Example

Let us look at the example of variance to understand the concept better:

Suppose a teacher is calculating the value of a batch with ten students. Their scores on the Math test were 25, 45, 50, 36, 56, 48, 30, 54, 33, and 43. Therefore, the teacher wants to measure the spread or distance between each student's scores.

Step 1: Calculation of mean value

Mean = Sum of all scores/ number of students

= (25+45+50+36+56+48+30+54+33+43)/10

= 42

Step 2: Applying the mean value to the formula

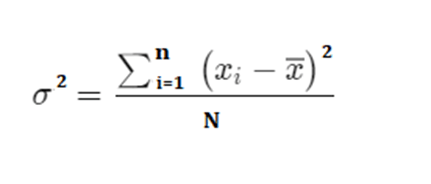
Applying the mean value to the formula
= ((25-42)² + (45-42)² + (50-42)² + (36 - 42)² + (56 - 42)² + (48 - 42)² + (30 - 42)² +  (54 - 42)² + (33- 42)² + (43 - 42)²)/10
 
= 1000/10
= 100

Graph

Let us look at the graphs to understand the concept better:

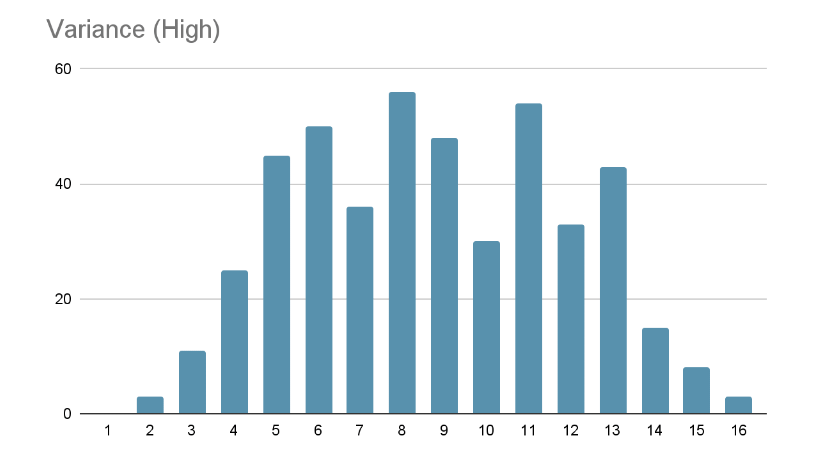
Variance Graph 1
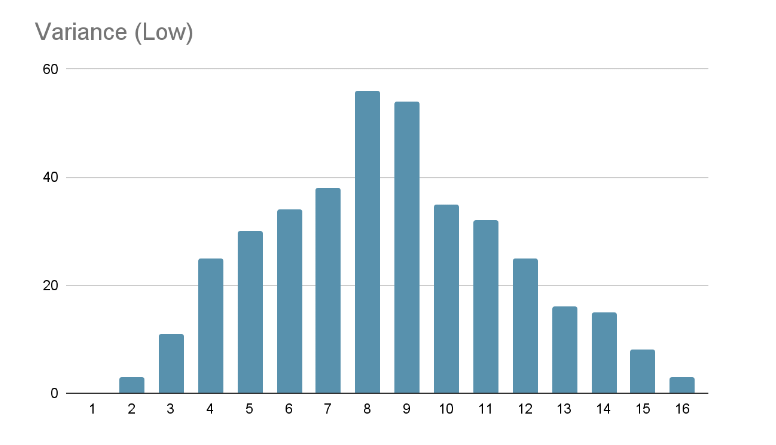
Variance Graph 2

In figure 1, most data points are far away or spread out from the Mean. However, in the case of figure 2, most points are gathered around the Mean. Thus, as per the theory, the initial figure has a high variance, and the latter has a lower value.

Variance vs Covariance vs Variability

Although variance, covariance, and variability are statistical methods for measuring variables, they have differences. The former is a parameter to check how a single variable deviates from the average data points. Here, the calculation can occur on both a sample and population basis.

However, covariance differs as it measures the movement of two variables or data points about each other. In contrast, variability is a broader concept encompassing various measures of dispersion and spread, such as range, standard deviation, quartiles, etc.

BasisVarianceCovarianceVariability
MeaningIt measures the degree of variability of a single variable from its mean.Covariance measures the degree to which two variables change together.Variability measures the extent to which the data points diverge from each other.
PurposeTo measure how the data points differ from the mean.To gauge the movement of the variables from each other.To measure how the points vary.
IncludesSample and populationPositive and negativeRange, standard deviation, quartile, and others.

Frequently Asked Questions (FAQs)

What are variance and variation?

Variance and variation are statistical terms used to describe the dispersion of a set of data points. Variance measures how much individual data points vary from the average value of the set and is calculated by averaging the squared differences between each data point and the mean. Variation is a more general term that refers to the extent to which data points differ, including differences in value, location, or pattern. 

What are the types of variances?

There are two types of it: population and sample variances. Population variance is the variance of the entire population, while sample variance is the variance of a subset of the population, known as a sample. In practice, sample variance is used more frequently since collecting data from the entire population is often impractical. So instead, researchers use statistical sampling to collect a representative subset of the population.

How to do variance analysis in statistics?

Variance analysis is a statistical technique that analyzes the difference between actual and expected values in a dataset. To perform the analysis, one should identify the dataset, calculate the mean value, and then the variance by finding the average of squared differences. Finally, one can conclude from the analysis results about the dataset's variation and clustering of data points.