Unbiased Expectations Theory

Published on :

21 Aug, 2024

Blog Author :

Edited by :

Reviewed by :

The unbiased expectations theory states that an investor will earn the same return from two individual one-year bonds as a single two-year bond. The theory is used to determine the short-term interest rate in the future based on the current long-term interest rates.

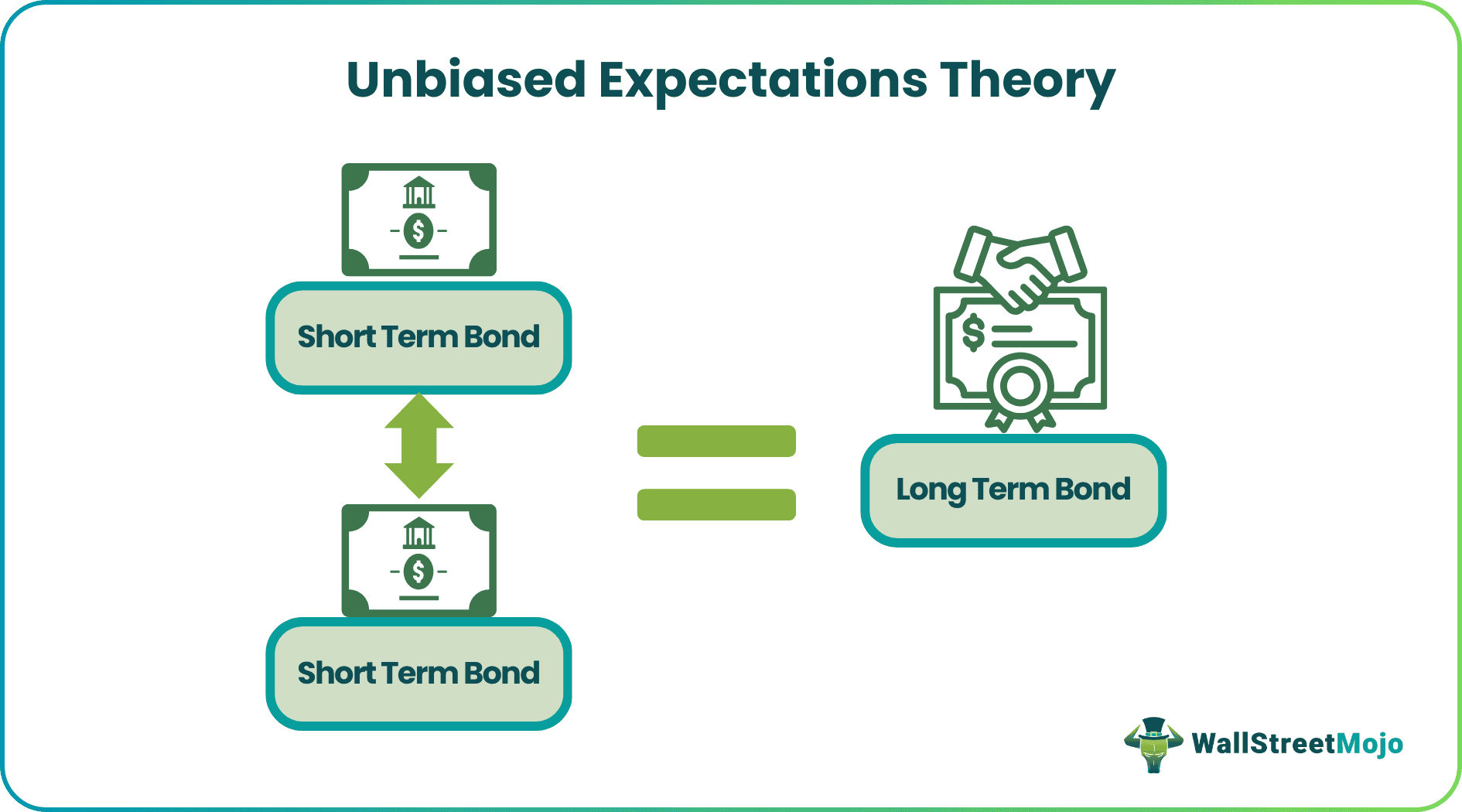
According to the unbiased expectations theory, individual one-year bonds will have separate low-interest rates compared to the single two-year bond. Still, due to compound interest, the investor will realize the same returns, and the net income will be equal. It implies that current long-term interest rates help predict future short-term interest rates.

What Is The Unbiased Expectations Theory?

Unbiased expectation theory states that the return for two short-term bonds is the same as one long-term bond of total duration. It determines the future short-term interest rates based on long-term interest rates.
It is not considered accurate for its inability to factor in the various internal and external factors and conditions that influence the financial market.
Investors use it to compare the bond yield and decide whether to invest in a long-term bond or replace it with a series of short-term bonds.
Ultimately, it is often treated as just a theory because it can only be applied to a market with equilibrium which is a rare case scenario.

The Unbiased Expectations Theory Explained

The unbiased expectations theory states that if there are two investors, one invests in two consecutive one-year bonds and the other invests in a single two-year bond, in the end, the return will be the same for both investors. Following the simple calculation, the theory plays a key role for investors willing to predict future short-term interest rates based on the current long-term interest rates.

According to the unbiased expectations theory, an investor can either purchase a current bond and hold it to maturity to enjoy the spot yield every year till maturity, or they can buy a series of one-year bonds in which only the spot yield will be known. Still, an investor can expect to determine the unknown future yield. One of the critical problems with this theory is that it only works when the market is at an equilibrium.

The investors take the help of the yield curve, which looks at the bond yield versus the maturity time. The yield curve typically has three graphical representations; it is a normal curve, which refers to a rising bond yield; if it is flat, it means a fixed bond yield; and in case it is inverted, it means the longer the maturity, the lower the bond yield will be. Based on this, the investor can decide whether to stay invested in a long-term bond or exit from it to opt for a series of one-year bonds. It is also possible to predict the future interest rate by following simple calculation steps. The theory is helpful but unreliable due to many limitations and assumptions. Therefore, investors should also use other methods.

How To Calculate?

There is no particular unbiased expectations theory formula, but simple steps are employed to predict future short-term interest rates.

Steps:

1 - Add 1 to the interest rate of a two-year bond.

2 - Calculate the square of the result.

3 - Divide the outcome with the present one-year interest rate after adding 1.

4 - Finally, subtract one from the determined value to determine the predicted one-year interest for the next year.

Examples

Here are two illustrative examples of the unbiased expectations theory:

Example #1

Suppose Howard is planning to invest in bonds and is searching for the right ones suitable for his short-term and long-term planning. While searching, he comes across the unbiased expectations theory, which can help him predict the market's future interest rates.

Howard currently has a two-year bond with an interest rate of 18% and contrary to which has a one-year bond that offers 15.3%

Now, Howard implies the unbiased expectations theory formula and steps -

1 + 0.18 = 1.18

Upon squaring,

1.18 x 1.18 = 1.392

Dividing the result with the one-year bond market rate after adding 1

1.392/1.153 = 1.20

Subtract one from the last value.

1 - 1.20 = 0.20 = 20%

Therefore, Howard earns a return equal to the present two-year bond's interest rate. If he invests in a one-year bond at 15.3%, the yield for the following year's bond would require an increase of up to 20% for his investment to become profitable.

Example #2

A similar example would be if given a two-year bond with an interest of 14.4% with a one-year bond offering 11.7%

Following the same steps again

Adding 1 to the two-year bond interest rate

1 + 0.144 = 1.144

Taking the square of the value

1.144 x 1.144 = 1.30

Dividing the outcome with the one-year bond market rate after adding 1

1.30/1.11 = 1.17

Subtracting one from the result

1 - 1.17 = 0.17 (17%)

In this scenario, the investor will receive a return equivalent to the current two-year bond's interest rate. If he/she invests in a one-year bond at 11.7%, the yield for the upcoming year's bond would need a hike of up to 17%.

Unbiased Expectations Theory vs Liquidity Premium Theory

Both theories help investors observe the pros and cons of a particular alternative. However, there are differences between the two, which have been mentioned below:

The unbiased expectations theory conceptualizes predicting future interest rates based on long-term interest rates. In comparison, the liquidity premium theory indicates the risk and reward of investment.
It does not account for several external market factors that impact the market interest rates. In contrast, the liquidity premium theory assumes an upward-sloping yield curve.
It is used to predict future bond yields. On the other hand, liquidity premium theory is employed to gauge the additional risk premium depending on the investment type.

Frequently Asked Questions (FAQs)

1. What are the advantages of unbiased expectations theory?

The benefits of unbiased expectations theory are -
- It helps investors predict the future bond market interest rates.
- Based on the determination, investors can compare two or more bonds or assets based on their yield and potential return.
- It eliminates the arbitrage factor as it follows that long-term interest rates can be predicted from short-term interest rates.

2. What are the assumptions of unbiased expectations theory?

The assumptions of unbiased expectations theory are -
- It assumes that the present long-term interest rates influence the future short-term interest rates.
- The theory does not consider the changing and dynamic market conditions and believes it is always relevant.

3. What are the limitations of the unbiased expectations theory?

The limitations of unbiased expectations theory are -
- Overestimation of future interest rates.
- It is often inaccurate in predicting the bond yield curve.
- The theory's assumption does not account for internal and external market factors which can mislead investors.