Type II Error

Last Updated :

Blog Author :

Edited by :

Reviewed by :

Table Of Contents

What is a Type II Error?

Type II error, commonly referred to as ‘β’ error, is the probability of retaining an incorrect factual statement. It is an error of a false positive, i.e., a statement is factually false, and we are positive about it.

What is a Type II Error?

Type II error refers to the likelihood of remembering an inaccurate factual statement. It is a false positive error, meaning we are sure that a message is untrue while being factually wrong.
Type mistakes are frequently used to establish a hypothesis, decide on a course of action based on the likelihood that they would occur, and pinpoint the factual rectification of the data that formed the idea.
Accepting false information is a Category II error while rejecting a true statement is a Type I error. This inaccuracy can be dangerous in business because the entire study and experiment may need to be corrected.

Explanation

One commonly uses type errors to create a hypothesis, determine a solution based on the probability of their occurrence, and identify the factual correction of the data that structured the hypothesis.

The diagram shows the creation of a null hypothesis, alternative hypothesis, sample mean, and error probability.

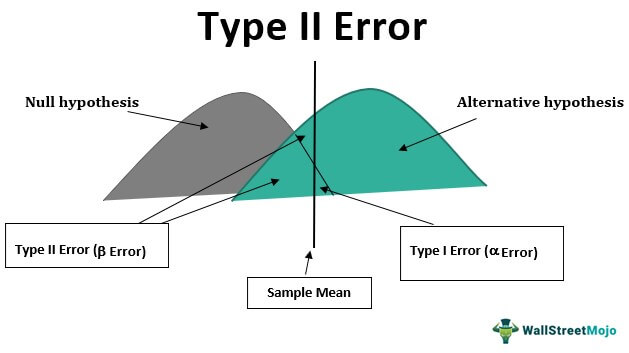
Every test we undertake always has a probability of error in decision-making, and such a decision may be a Type I or Type II error. In simple words, while undertaking decision-making, we might reject the correct facts or accept the wrong facts. Rejection of correct facts is a Type I error, and accepting incorrect facts is a Type II error. This error can be very dangerous in the corporate world as the complete analysis and experiment can get wrong if the base itself is wrong.

Following is the matrix of which type of error one might undertake if facts are wrongly accepted:

	A decision was taken to Retain		A decision was taken to Reject

	( Positive)		( Negative)
Null Hypothesis is true		True Positive		True Negative
	(1- a)		= Type I error
Null Hypothesis is False		False Positive		False Negative
	(β) = Type II Error		(1 – β)

A decision was taken to Reject

Example of Type II Error

In human beings, women tend to get pregnant. However, while verifying, a doctor mistakenly diagnoses a man to be pregnant. It is a Type II error, where the base itself was wrong.
Suppose the doctor diagnoses a woman as not pregnant when she is pregnant. It is a Type I error, where the facts are correct, but the one rejects the same.

How Does Type II Error Occur?

Various factors may result in such an error.

#1 – Any change in the population is comparatively very small to detect

If the tendency to change is not visible in the population itself, then any hypothesis testing will not be able to cater to the correct facts. Such a scenario will lead to accepting incorrect facts, resulting in Type II errors.

#2 – Sample size covers a very small portion of the population

The sample selection should represent the whole population. Thus, if the sample is not an ideal population representation, it is highly unlikely to give the correct analysis. The analyst will not be able to identify the correct facts. As a result, they will rely on the wrong facts, resulting in a Type II error.

#3 – Incorrect sample selection

Generally, one uses random sampling worldwide as it is considered one of the most unbiased sample selection methods. However, many times, it results in the wrong picking of samples. As a result, it leads to incorrect population coverage and results in a Type II error.

Can Type II Errors Be Avoided?

#1 – Repeat analysis until one reaches the required significance

Significance specifies whether the null hypothesis is factually correct or not. At the end of all analyses, one accepts the null hypothesis and ensures that the facts are correct. However, often, only a single analysis cannot achieve such significance. This unilateral analysis may result in Type I or Type II errors. On the other hand, if the same kind of output comes in the repetitive analysis, one will ensure no errors occur.

#2 – In each repetition of analysis, change the size of the test of significance

As discussed in point 1, significance shows the appropriateness of the null hypothesis. If one finds that the sample is not adequately covered, one can reiterate that the size of significance increases. It will help understand the behavior and avoid a Type II error.

#3 – Alpha level around 0.1 is the ideal

Generally, an alpha of around 0.1 will result in the rejection of the hypothesis. Any rejection will allow multiple verifications. As a result, the chances of occurrence of errors reduces. Type II error occurs when anything gets wrongly accepted. If there is no scope for acceptance, such an error will not occur.

Importance

It is more dangerous as compared to Type I errors.
Any analysis can get worked out on a few necessary details and underlying assumptions. At the end of a hypothesis, one can determine whether the test statistic is in line with the given fact or not. Such test specifics will display whether the sample means are equivalent to the population mean.
If the null hypothesis appears to reach significance due to some error in the analysis, one can accept the fact in the null hypothesis.
However, such a null hypothesis ought to be unacceptable in actuality. As a result, one must be highly sure while accepting the null hypothesis statement. By re-verifying it, one can get better significance to boost the correctness of fact.

Type I Error vs Type II Error

Following are the basic difference between the two types of error:

Sr No	Type I error	Type II error
1	It occurs when the correct null hypothesis is not accepted.	It occurs when an incorrect null hypothesis is getting accepted
2	Such errors are truly negative.	Such errors are false-positive
3	It is denoted by alpha.	It is denoted by Beta
4	Null hypothesis and type 1 error	Alternative hypothesis and type 2 error
5	If the resultant effect of this error is worse than a Type I error, one should consider alpha with a value higher than 0.10	If the resultant of a Type I error is worse, one should set alpha with a value lower than 0.01.

Conclusion

Type II error is a false negative resulting from accepting an incorrect null hypothesis. In the practical world, such errors fail the full project as the base is inaccurate. Moreover, such a base may be like details, facts, or assumptions, jeopardizing the complete analysis.

Frequently Asked Questions (FAQs)

The type II error rate would be lowest with?

This error rate will be lowest when the sample size is sufficiently large, the significance level is appropriately chosen, the effect size of the phenomenon being studied is large, and the variability of the data is low.

When is there a risk of a type II error?

The risk of this error depends on several factors, including the sample size, the level of significance chosen for the test, the effect size of the phenomenon being studied, and the variability of the data.

What does a high type II error mean?

Type II errors resemble "false negatives," the inaccurate conclusion that a test change did not make a statistically significant impact. According to statistics, you erroneously accept the incorrect null hypothesis and assume a relationship doesn't exist when it does.

What does * represent in a type II error?

When you accept the null hypothesis even when it is wrong, a type II error represents the likelihood of a type-II error. The consumer's risk of not rejecting a potentially useless good or service, as suggested by the null hypothesis, is how type-II errors are sometimes referred to.