Two-Way ANOVA

What Is a Two-way ANOVA Test?

The ANOVA (Analysis of variance) test compares the means of different samples and the significance of their differences. A two-way ANOVA test is a statistical analysis tool that determines the effect of two variables on an outcome, as well as testing how altering the variables will affect the outcome.

Suppose a farmer wants to find the best combination of potato strain and fertilizer that will bring him the greatest yield. The two-way ANOVA test helps him find this, along with telling him how the two factors influence the outcome. Here, the two variables are the potato strains and the fertilizer.

• The two-way ANOVA test is a statistical test used to determine the effect of two variables on an outcome.
• The two-way ANOVA test is used in numerous industries, including commerce, medicine, and social science.
• Some assumptions need to be considered when carrying out the two-way ANOVA test. Ensuring that your data conforms to these assumptions increases the quality of the results

How Does Two-way ANOVA Test Works?

The two-way ANOVA test is an extension of the one-way ANOVA test, although the latter is a more hypothetical one. An ANOVA test determines whether a statistical operation has outcomes that are useful or not. In essence, it allows one to determine whether to reject or accept a null hypothesis. In a two-way ANOVA test, two variables are used to determine this. 

The two-way ANOVA test reveals whether the two important variables affect the outcome or a dependent variable. One can then use the result to work out variances and to carry out an f-test. The two-way ANOVA test is similar to the two-sample t-test but has the benefit of having a lower chance of getting type 1 errors, which could corrupt the data collected. The two-way ANOVA is versatile; it can compare means and variances within-subjects, between groups, within groups, and even between test groups. 

An example of using the two-way ANOVA test is researching types of fertilizers and planting density to achieve the highest crop yield per acre. To do such an experiment, one could divide the land into portions and then assign each portion a specific type of fertilizer and planting density. Once the crop is mature, the yield in each plot is measured. The two-way ANOVA test then determines which combination of fertilizer and crop density yields the best harvest and how the two variables affect the outcome. 

The two-way ANOVA test has many applications in areas including commerce, public health, medicine, pharmacy, and social science.

Assumptions of Two-way ANOVA

When using the two-way ANOVA test, a person must make several assumptions, including: 

• Independence of variables: The two variables for testing should be independent of each other. One should not affect the other, or else it could result in skewness. This means that one cannot use the two-way ANOVA test in settings with categorical variables.
• Homoscedasticity: In a two-way ANOVA test, the variance should be homogenous. The variation around the mean for each set of data should not vary significantly for all the groups.
• Normal distribution of variables: The two variables in a two-way ANOVA test should have a normal distribution. When plotted individually, each should have a bell curve. If the data does not meet this criterion, one could attempt statistical data transformation to achieve the desired result.

Example

Suppose we want to explore how a detergent and a particular water temperature affect the dirt removal of laundry. We also want to check if the combined effect of detergent and water temperature can affect the dirt removal. Here, we have two types of detergents, namely x and y. We also use three types of water temperatures, the levels of which are cold, warm, and hot. Here the detergent and the water temperature are independent variables, while the amount of dirt removed (D) is the dependent variable. We are using a two-way ANOVA instead of one-way ANOVA because we have two factors with multiple levels in hand, i.e., detergent and water temperature. 

With each combination, one would wash five loads, which shall be replicates. Suppose we record the information as:

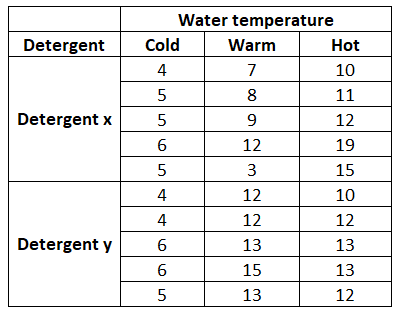
The numbers denote the amount of dirt removed (D)

The null hypotheses would be:

• The type of detergent does not determine the amount of dirt removed.
• The temperature does not determine the amount of dirt removed.

The solution for the two-way ANOVA test in Excel would be:

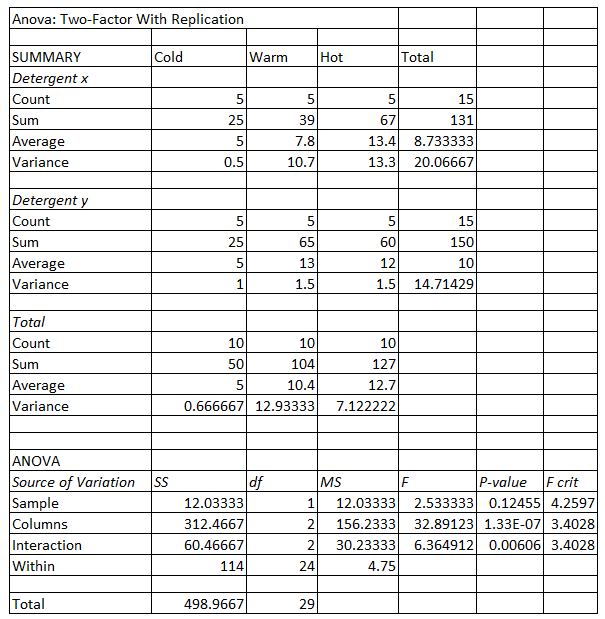
The table above can find the optimal combination of temperature and detergent used to get the cleanest wash. 

Interpretations

In using a two-way ANOVA test, if the main effect of one factor is significant following the f-test, then it means that the difference between some of the level averages is statistically significant. However, if an interaction term is significant, the relation between the response variable and the factor differs by an amount equal to the other factor. In such a case, one should not interpret the main effects without considering the effects of the interactions. 

In the table above, the p-value of interaction between detergent and water temperature is 0.006, which is insignificant at an alpha level 0.05. This means that one can ignore the interaction effect between the two factors. On the other hand, the p-value of water temperature is 1.33E-07 which is significant at the alpha level of 0.05. This indicates that the water temperature has a consistent impact on the amount of dirt removed from the laundry. 

Frequently Asked Questions (FAQs)

Recommended Articles

This has been a guide to the Two-Way ANOVA test. Here we discuss how a Two-Way ANOVA test works along with an example, assumptions, and interpretations. You may also have a look at the following articles to learn more.

• ANOVA in Excel
• Regression vs ANOVA
• Degrees of Freedom