Table Of Contents
About Traditional IRA Calculator
The formula for calculating Traditional IRA is per below:
Periodical Traditional IRA is made then:
When an investment is made at the beginning of the period
Wherein,
- A is the starting account balance
- E is the periodical fixed amount invested at regular intervals
- r is the rate of interest
- F is the frequency of interest is paid
- n is the number of periods for which a traditional IRA shall be made.
IRA stands for an Investment Retirement Plan and is used by individuals for accumulating savings and deferred the tax payment until the age of retirement so that when the individual is in a lower tax bracket, they would be paying fewer taxes and at the same time deferring the payments.
Even contribution in an investment retirement account can be a tax benefit that is by taking a deduction of the amount that is contributed, and hence it would be tax-deferred growth. The individual thus can avoid paying higher taxes on the savings they have made and accumulate higher funds for their retirement. Traditional IRA Calculator can be used to calculate the maturity amount that will be received during the time of retirement, which would be accounted for taxes as well at the time of retirement.
How to Calculate using a Traditional IRA Calculator?
One needs to follow the below steps in order to calculate the maturity amount.
Step #1: Determine the initial balance of the account, if any, and also, there will be a fixed periodical amount that will be invested in the Traditional IRA.
Step #2: Figure out the rate of interest that would be earned on the Traditional IRA.
Step #3: Now, determine the duration left from the current age until the age of retirement.
Step #4: Divide the rate of interest by the number of periods the interest or the Traditional IRA income is paid. For example, if the rate paid is 7% and it compounds annually, then the rate of interest would be 7%/1, which is 7.00%.
Step #5: Now, use the formula that was discussed above for calculating the maturity amount of the Traditional IRA, which is made at regular intervals.
Step #6: The resultant figure will be the maturity amount that would include the Traditional IRA income plus the amount contributed.
Step #7: There could be tax liability at the time of retirement, which should be accounted for accordingly.
Examples
Example #1
Mr. A has been contributing $5,000 every year in an investment retirement account so as to accumulate funds during his retirement. He is currently 32 years old, and the retirement age is 65 years. He currently falls under a 25% tax bracket, and he is estimating a 12% tax bracket at the time of retirement for his investment income.
He is also eligible for a tax deduction for the amount he is contributing every year. The investment would fetch him 5% per annum. His total gross income for the year is $45,000. There has been no account balance in his IRA account till now. The Amount is distributed at the beginning of the year.
Based on the given information, you are required to calculate the amount that would be accumulated at the time of maturity.
Solution:
We are given the below details:
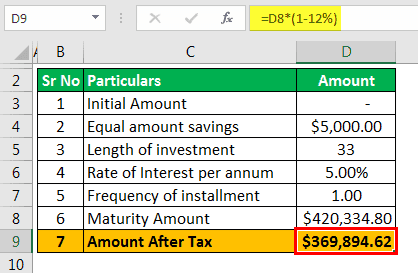
| Sr No | Particulars | Amount |
|---|---|---|
| 1 | Initial Amount | - |
| 2 | Equal amount savings | $5,0000.00 |
| 3 | Length of Investment | 33 |
| 4 | Rate of Interest per annum | 5.00% |
| 5 | Frequency of Installment | 1.00 |
- A = NIL
- E = Fixed amount deposited periodically, which is $5,000
- r = Rate of interest, which is 5.00% and is compounded annually
- F = Frequency which is annually here, hence it will be 1
- n = number of years the Traditional IRA proposed to be made will be different from retirement age less current age (65 – 32), which is 33 years.
Now, we can use the below formula to calculate the maturity amount.

- = 0 * ( 1 + 5.00% )1 * 33 + $5,000 *
- = $4,20,334.80
At the time of retirement, he will be in the tax bracket of 12% and hence the amount that will be received post-tax will be

- = $4,20,334.80 * ( 1 – 12%)
- = $3,69,894.62
Example #2
Mrs. P has been staying in the states for almost a decade now and she will be celebrating her 40th birthday next month and she is worried as to why she hasn’t planned for her retirement. Her friend advises her to invest in an IRA account since she has been a risk-averse person throughout her life. She decides to contribute per year $12,500 which is 10% of her total income.
She is currently paying taxes at a rate of 25%, and her friend has told her by the time she retires, she would be liable only for an 8% tax. She is planning to retire by the age of 65 years. She does her contribution at the start of the year. She already had $30,567 as of account balance which she hasn’t touched for a couple of years. The IRA account pays 4% compounded annually.
Based on the given information, you are required to calculate the maturity amount.
Solution:
We are given the below details:
| Sr No | Particulars | Amount |
|---|---|---|
| 1 | Initial Amount | $30,567.00 |
| 2 | Equal Amount Savings | $12,500.00 |
| 3 | Length of Invesment | 25 |
| 4 | Rate of Interest per annum | 4% |
| 5 | Frequency of Installment | 1.00 |
- A = $30,567
- E = Fixed amount deposited periodically, which is $12,500
- r = Rate of interest, which is 4.00% and is compounded annually
- F = Frequency which is annually here, hence it will be 1
- n = number of years the Traditional IRA proposed to be made will be different from retirement age less current age (65 – 40), which is 25 years.
Now, we can use the below formula to calculate the maturity amount.

- = $30,567 * ( 1 + 4.00% )1 * 25 + $12,500 x
- = $ 6,22,883.43
At the time of retirement, he will be in a tax bracket of 8% and hence the amount that will be received post-tax will be

- = $ 6,22,883.43 * ( 1 – 8%)
- = $5,73,052.75
Conclusion
As discussed, an individual can use the IRA account to defer the savings for their retirement and also defer their tax and save tax by taking a deduction of the amount contributed. The individual can thus save the taxes by paying lower taxes at the time of retirement.