TAN Excel Function (Tangent)

The TAN Excel function is a built-in function categorized as a Math/Trig function, which returns the tangent of an angle. The formula for TAN always returns a numeric value.

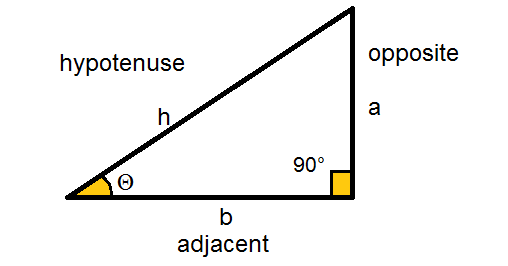
In trigonometry, a tangent of an angle is equivalent to the ratio of the perpendicular to the base of a right-angled triangle.

TAN Θ = opposite side/ adjacent side

Therefore, TAN Θ = a/b

Table of contents

Below is the formula for TAN in Excel.

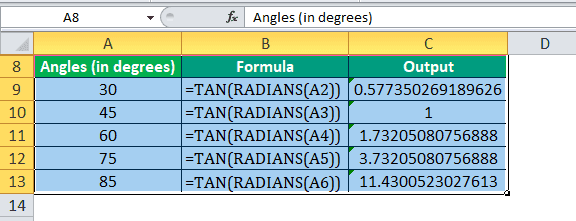
Here, a number is an argument passed to the function in radians.

The angle we specify as input is recognizable by the TAN function only when defined as radians.

To convert an angle into radians, use the RADIANS function or convert the angle into radians by a mathematical relation.

Radian = angle degree * (π/180)

π in Excel is represented by a function PI()

Therefore, radian = degree *(PI()/180)

Calculating TAN value using TAN and RADIANS functions:

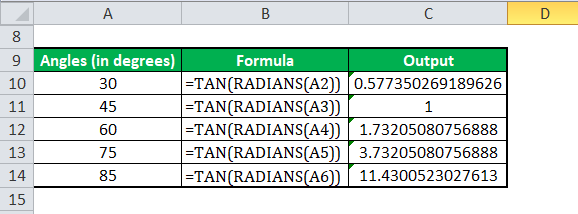
Calculating TAN value using TAN and PI functions:

The TAN function has many real-life applications. It is widely used in architecture to calculate the heights and lengths of geometric figures. The TAN function is used in navigation systems, GPS, and aeronautics.

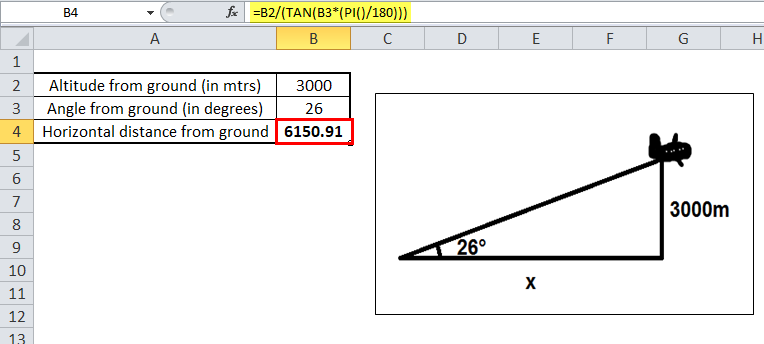
For example, if an airplane is flying at the height of 3,000m and it makes an angle to an observer on the ground of 26°, we want to find the plane's distance from the observer.

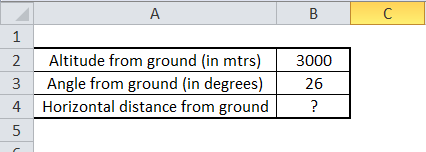
As we know that TAN Θ = opposite side/ adjacent side

Here, the opposite side = altitude of the plane from the ground, equal to 3000 meters.

And the adjacent side = horizontal distance of the plane from the ground, which is unknown, and we need to calculate it.

So using the formula for TAN, we have:

TAN(26°) = 3000/x

Therefore, x = 3000/(TAN(26°))

In Excel, taking the relative reference values, we have,

X =B2/(TAN(B3*(PI()/180)))

X= 6150.91 meters

Excel TAN function is very simple and easy to use. Let me understand the working of the formula for TAN in Excel by some examples.

A man with a height of 6 feet is 55 meters from a tree. He makes an angle of 47° for the vision parallel to the ground. We want to calculate the height of the tree.

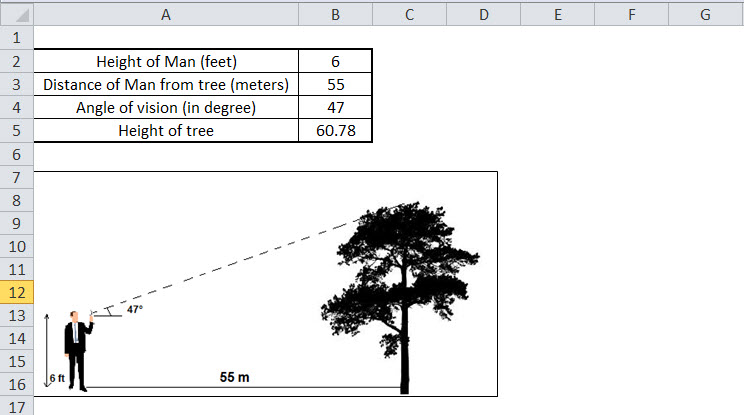
To find the tree's height, we will use the TAN Θ. In the context of Excel, we will be using the tangent function.

The height of the tree will be:

The Height of Man + Distance of Man from tree * TAN(47°)

Since the height of the man is in feet so we will convert it into meters (1 foot = 0.30 meters)

Putting all the relative values in Excel, the formula for the height of the tree will be:

=(0.3*B2)+(B3*TAN((B4*(PI()/180))))

TAN Excel Output:

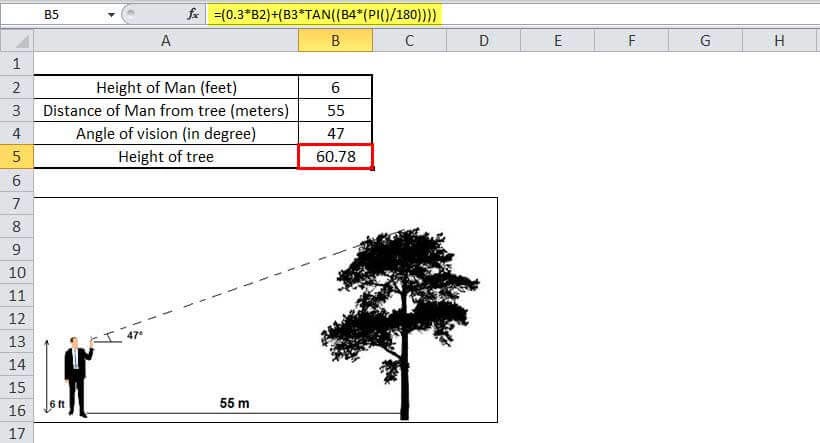
The height of the tree is 60.78 meters.

Suppose we have five right-angled triangles, given their angles and length on one side, and we need to calculate the length of the other two sides.

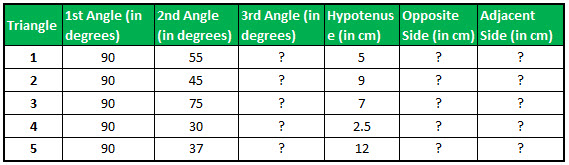
The sum of all the angles on a triangle is equal to 180.° Therefore, we can easily calculate the third angle.

We know Sin Θ = Opposite/Hypotenuse.

So, the opposite side length will be Sin Θ * Hypotenuse.

In Excel, the length of the Opposite side (perpendicular side) will be calculated by the TAN formula:

=E2*SIN(C2*(PI()/180))

Applying the TAN formula for five triangles, we can get the length of perpendiculars of the triangles.

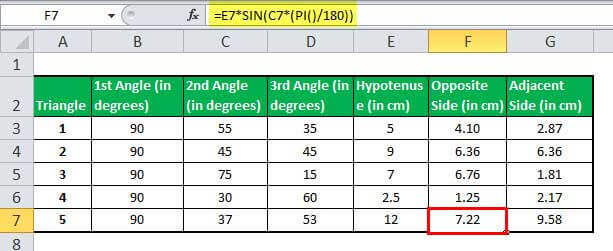
Now, we have two sides of the triangle, the hypotenuse, and the perpendicular side. Using the TAN in Excel, we can easily calculate the third side (base).

We know TAN Θ = Opposite side/Adjacent side.

So, the adjacent side length will be Opposite Side/TAN Θ.

In Excel, the TAN formula will calculate the length of the adjacent side (base).

=F2/(TAN(RADIANS(C2)))

Applying the TAN formula for five triangles, we can get the length of the adjacent side of the triangle.

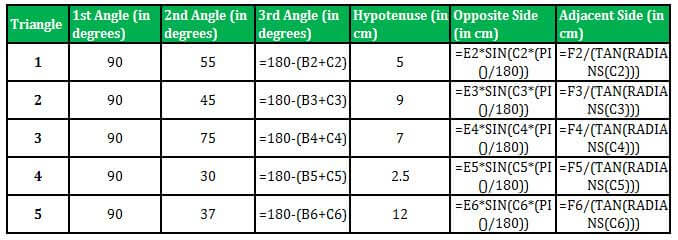
TAN in Excel Output:

An aircraft takes a turn of a radius of 160 m and flies with a constant bank angle of 87°. Then, in ideal conditions (no wind fluctuations), calculate the constant ground speed of the aircraft.

The formula gives the radius of the turn.

Radius of turn = V2/ g * TAN Θ

The radius of turn is 160 meter; the Constant bank angle is 87°, g is the acceleration of gravity whose value is 9.8 m/s², so the ground speed will be:

V = (Radius of turn * (g * TAN Θ))^1/2

Applying the above TAN formula in Excel with the reference values, we have the TAN formula:

=SQRT(B2*(9.8*(TAN(RADIANS(B3)))))

SQRT is an Excel built-in function that computes the square root of a number.

TAN in Excel Output:

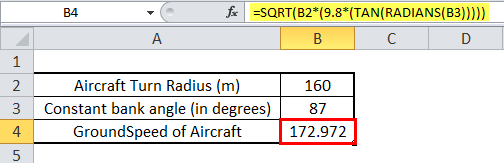
So, the ground speed of the aircraft is 172.97 m/s.

We have a formula for TAN denoted by f(x) = 2c*TAN2Θ, where the c is a constant value equal to 0.988. The variant value is the value of Θ, and the formula for TAN depends on the value of Θ. First, we need to plot the graph of the given tangent function.

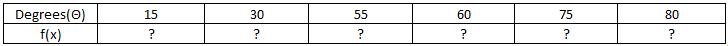
Using the Excel TAN function, we will then calculate the values of the function, so taking the reference values as input, we have the TAN formula:

=2*0.988*(TAN(RADIANS(2*B3)))

Applying the TAN formula to other cells, we have:

TAN in Excel Output:

Tangent Function Graph: