T-test in Excel

The syntax of the TTEST function is shown in the following image:

The TTEST function accepts the following arguments:

• Array1: This is the first dataset on which the excel t-test is to be performed.

• Array2: This is the second dataset on which the excel t-test is to be performed.

• Tails: This specifies the kind of distribution to be used. This argument can take either of the following values:
  • 1–This implies a one-tailed distribution. A one-tailed t-test is performed when one wants to study the specific direction (only positive direction or only negative direction) of difference between the two means.
  • 2–This implies a two-tailed distribution. A two-tailed t-test is performed when one wants to find out whether the two population means are different from one another or not.

• Type: This is the kind of t-test to be performed. This argument can take any of the following values:
  • 1–This implies that a paired samples t-test is to be performed.
  • 2–This implies that a two-sample equal variance t-test is to be performed. One must perform this test when there are two independent samples having the same (equal) population variances. The feature of the same variance is known as homoscedasticity.
  • 3–This implies that a two-sample unequal variance t-test (or the Welch t-test) is to be performed. One must perform this test when there are two independent samples having unequal or unknown variances. The feature of unequal variances is known as heteroscedasticity.

All the preceding arguments are mandatorily required when conducting a t-test in Excel.

Note: For information about the kind of t-tests, refer to the next heading, “types of t-tests.”

A t-test can be of the following types:

1. Independent samples t-test–It compares the means of two independent or unrelated samples or groups. It is also called an unpaired t-test or a two-sample t-test. It is used when the population mean or standard deviation is unknown.
2. Paired samples t-test–It compares the means of the same group at different time periods. In other words, the t-test is conducted on dependent or related samples. The paired samples t-test is also conducted when the samples are different but subjected to the same conditions. For instance, one may want to measure the effectiveness (using the same technique) of the same product manufactured by two different manufacturers. The paired samples t-test is also called the dependent samples t-test.
3. One-sample t-test–It compares the mean of a single sample with the known mean (target value or hypothetical value) of a population (from which this sample is drawn).

Note 1: Select the type of t-test to be conducted by taking into account the kind of data and the kind of analysis required. For instance, if the two sample sets are related, use the paired t-test. Further, the paired samples t-test must be performed when both the sample sets are of the same size. This implies that the number of data points of both samples is the same.

If the samples are independent, use the two-sample equal variance or two-sample unequal variance t-tests depending on whether the variances are equal or unequal respectively.

Note 2: For more information on the type of t-test to be performed, refer to the heading “frequently asked questions” at the end of this article.

The TTEST function of Excel is simple and easy to use. Let us consider some examples to understand the working of the TTEST function in Excel.

Example #1–Paired Sample T-test Using One-tail Distribution

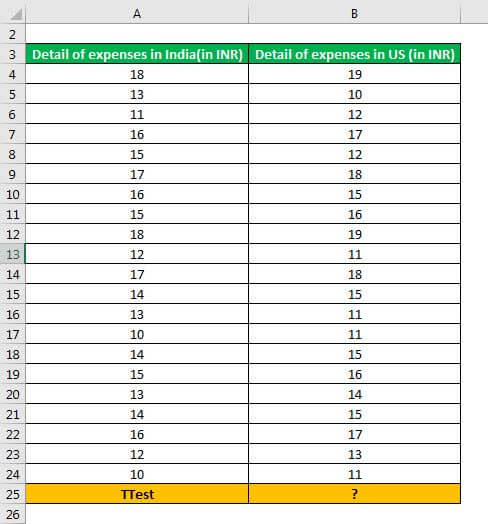
The following image shows the expenses incurred (in INR) by an organization in two countries, India and USA. Perform a paired sample t-test in excel using a one-tail distribution.

The steps to perform a paired t-test with one-tail distribution are listed as follows:

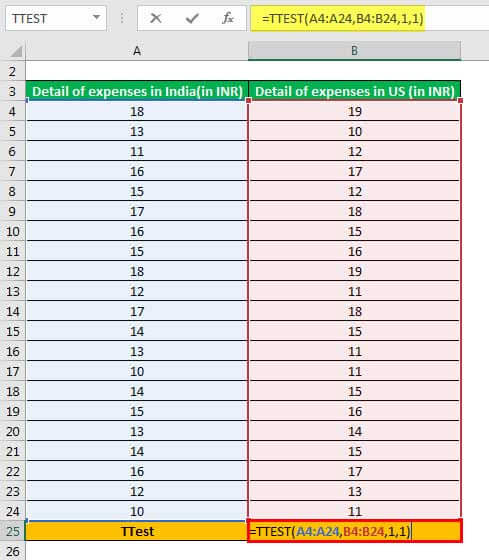
Step 1: Enter the following formula in cell B25.

“=TTEST(A4:A24,B4:B24,1,1)”

The same is shown in the following image.

Step 2: Press the “Enter” key. The output in cell B25 is 0.177639611, as shown in the following image.

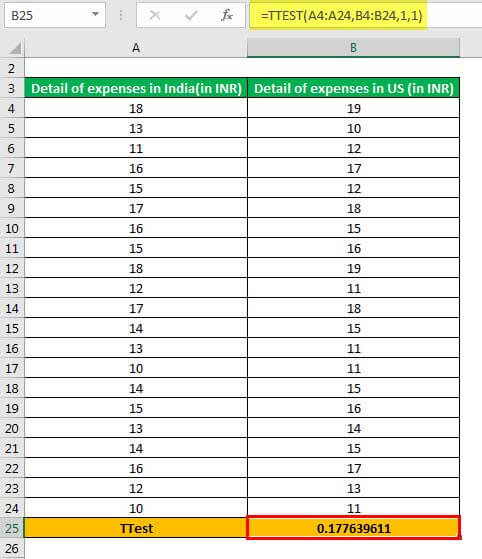
Explanation: The range A4:A24 (entered in step 1 of the formula) is the first array on which the excel t-test is to be performed. Likewise, the range B4:B24 is the second array on which the t-test is to be performed.

Further, we have entered the “tails” and “type” arguments as 1. This is because a one-tailed, paired t-test needs to be performed.

Interpretation: To accept or reject the null hypothesis, perform the following tasks:

1. Calculate the t-table value by referring to the one-tail t-distribution table, at a certain significance level (alpha) with the specific degrees of freedom (df). Compare the t-table value with the calculated t-value (0.177639611). If the calculated t-value is greater than the t-table value, reject the null hypothesis.
2. Calculate the p-value based on the t-table value. Compare the p-value with the significance level. Since the significance level (alpha) is not specified in the question, consider it as 0.05 or 5%. If the p-value is less than the significance level, reject the null hypothesis.

The acceptance or rejection of the null hypothesis should be carried out by using a combination of the p and t values (obtained in the preceding pointers a and b). Further, rejecting a null hypothesis implies accepting the alternative hypothesis.

Note 1: The negative sign (if any) can be ignored when comparing the t-values.

Note 2: The null hypothesis of a paired sample excel t-test assumes that the mean difference of paired observations is zero. In other words, the mean of paired observations is equal.

The alternative hypothesis of a paired sample t-test assumes that the mean difference of paired observations is not equal to zero. For instance, the difference between the paired observations for row 4 is (18-19) or (cell A4-cell B4).

Rejecting the null hypothesis implies that the mean difference of paired observations does exist. In other words, this mean difference is not equal to zero.

Example #2–Two-sample Equal Variance T-test Using One-tail Distribution

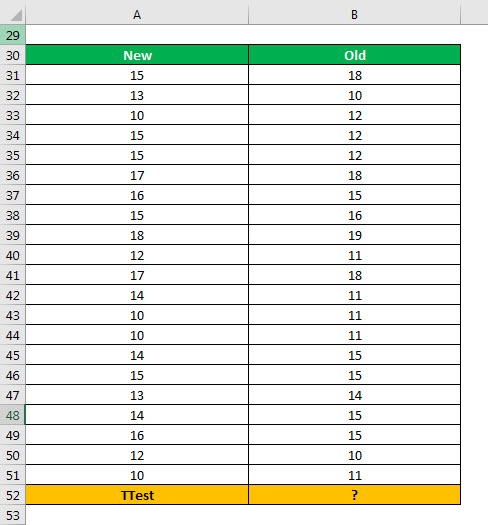
An organization has introduced a new flavor of a beverage in the market. To test the effectiveness of this flavor, two samples (consisting of 21 people in each sample) are created.

The different people who tasted the new flavor are listed in the column “new.” The different people who tasted the old flavor are listed in the column “old.” Consider the groups “new” and “old” as independent samples.

The population variances of both samples, “new” and “old,” are equal. Calculate the two-sample equal variance t-test in excel using a one-tail distribution.

The steps to perform the two-sample equal variance t-test using a one-tail distribution are listed as follows:

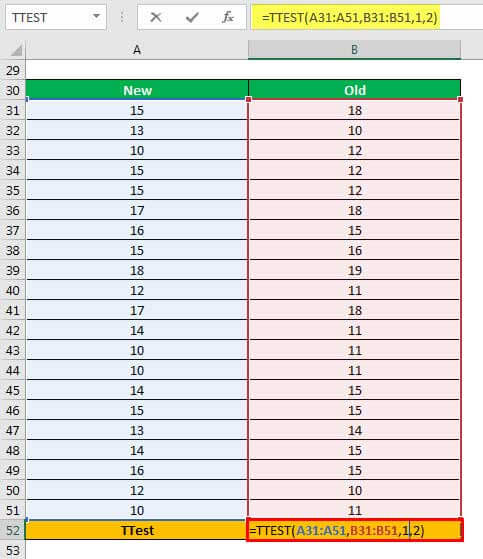
Step 1: Enter the following formula in cell B52.

“=TTEST(A31:A51,B31:B51,1,2)”

The same is shown in the following image.

Step 2: Press the “Enter” key. The output in cell B52 is 0.454691996.

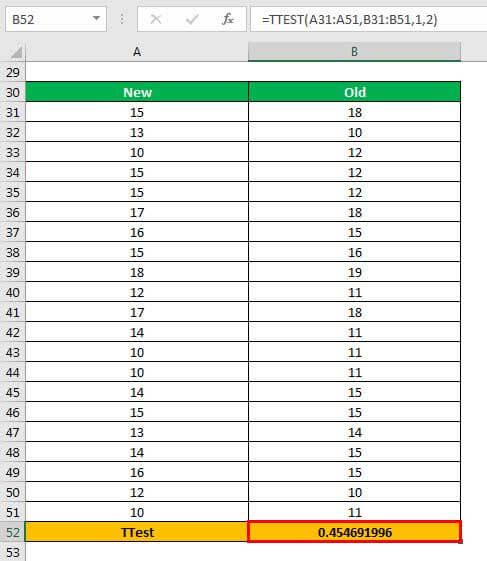
Explanation: The first array (in the formula entered in step 1) is A31:A51 and the second array is B31:B51. The argument 1 indicates that a one-tailed test is to be performed. The argument 2 implies that a two-sample equal variance t-test is to be conducted.

Interpretation: To accept or reject the null hypothesis, compare the calculated t-value with the t-table value. At the same time, compare the p-value with the standard significance level (0.05).

Note 1: The null hypothesis of the two-sample equal variance t-test in excel states that the difference between the two sample means is zero. In other words, the two sample means are equal. The alternative hypothesis states that the two sample means are not equal.

Note 2: If one is using the Data Analysis Toolpak, compare the t-statistic of the results obtained with the t-critical one-tail value. If the t-statistic is larger than the t-critical one-tail value, reject the null hypothesis.

Likewise, compare the p one-tail value with the significance level. If the former (p one-tail value) is less than the latter (significance level), reject the null hypothesis.

Rejecting a null hypothesis implies that there is a difference between the two sample means. Moreover, this difference is not explainable by chance alone.

Note 3: While using the Data Analysis Toolpak, if one does not know which t-values (of one-tail or two-tail test) are to be compared, always compare the t-statistic with the t-critical two-tail value.

Example #3–Two-sample Unequal Variance T-test Using One-tail Distribution

A researcher wants to study the impact of a new drug on the car driving skills of a person. A total of 21 individuals were administered the drug prior to being given a driving test.

The column A of the following image shows the score assigned to each driver. The column B shows the level of drug (in percentage) given to each driver.

The population variances of both the samples are unequal. Perform the two-sample unequal variance test using a one-tail distribution.

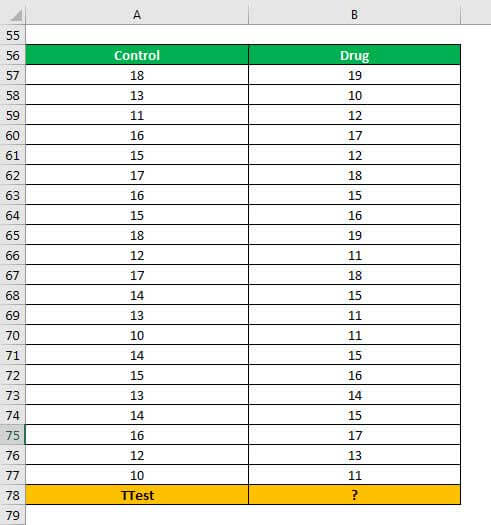
The steps to perform the two-sample unequal variance test using a one-tail distribution are listed as follows:

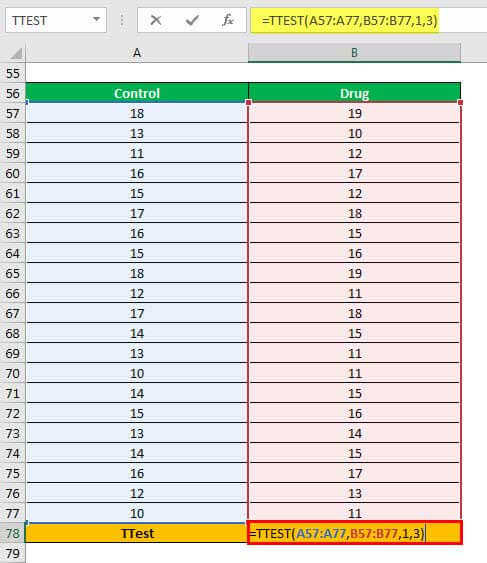
Step 1: Enter the following formula in cell B78.

“=TTEST(A57:A77,B57:B77,1,3)”

The same is shown in the following image.

Step 2: Press the “Enter” key. The output is 0.364848284, as shown in the following image.

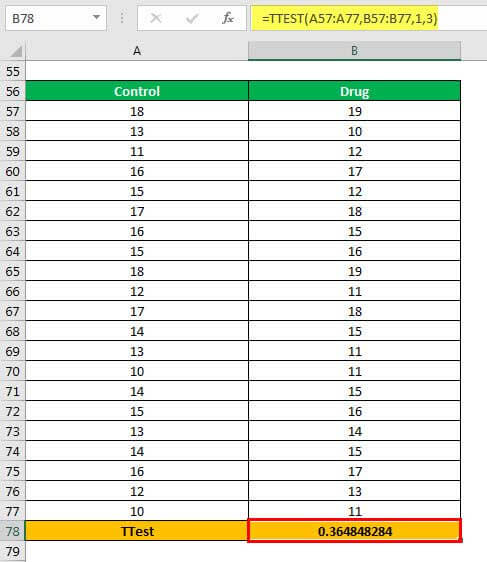
Explanation: The range A57:A77 represents the first array (in the formula entered in step 1). The range B57:B77 represents the second array on which the excel t-test is to be performed.

Since a one-tailed test is to be performed, we enter 1 in the “tails” argument. The 3 in the “type” argument implies that the two-sample unequal variance t-test is to be performed.

Interpretation: Compare the t-calculated value with the t-table value. If the former is greater than the latter at the given significance level, reject the null hypothesis. Likewise, if the p-value is smaller than the significance level, reject the null hypothesis and accept the alternative hypothesis.

Note: The null hypothesis for the two-sample unequal variance t-test states that the mean of the two samples is the same (or equal). The alternative hypothesis states that the mean of the two samples is not the same (or unequal).

Example #4–Paired Excel T-test Using One-tail Distribution in VBA

There are two datasets in the ranges A4:A24 and B4:B24 of Excel. Write the VBA code to conduct a t-test on the given ranges.

The VBA code is written as follows:

Sub TTESTcal()  // start the TTEST function scope

Dim TTEST as interger

TTEST = Application.WorksheetFunction.TTest(Range("A4:A24"),Range("B4:B24"),1,1)

MsgBox TTEST // print the TTEST value in the message box.

End sub // End the TTEST function

The TTEST function can return the following types of errors:

• “#N/A” error: This is displayed if the two arrays supplied are of different lengths and a paired t-test is to be performed.

• “#NAME?” error: This is displayed if either of the arguments “tails” or “type” is provided as a text value.
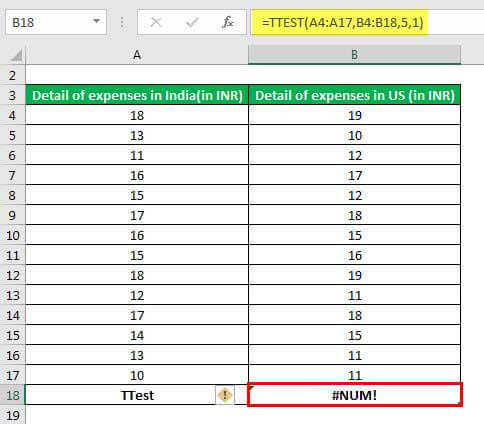
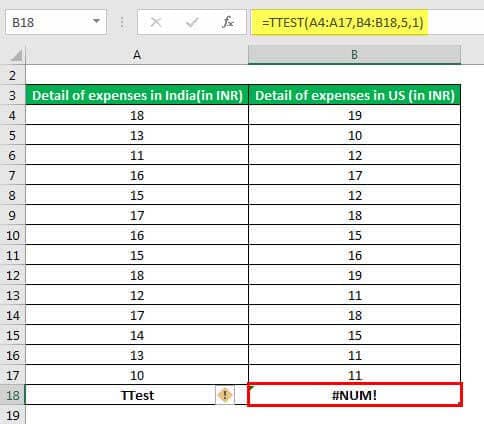
• “#NUM!” error: This is displayed on account of either of the following reasons:
  • If the “tails” argument is other than the numbers 1 or 2
  • If the “type” argument is other than the numbers 1, 2 or 3

The “#NUM!” error is shown in the following image. It must be observed that the “tails” argument in the TTEST formula has been entered as 5. Moreover, the two arrays supplied are of different sizes.

Had the arrays been equal in length and the “tails” and “type” arguments had remained 5 and 1 respectively, the “#NUM!” error would still have been displayed.