Table Of Contents
What is Supply Function?
The supply function in economics is a mathematical formula that depicts the relationship between quantity supplied, price of the commodity, and other related variables. Here, the quantity supplied is expressed as a function of the price. It helps businesses and governments to study and monitor an economy's demand-supply situation.
The supply function in economics is of utmost importance to businesses. They can establish the optimum quantity-price relationship to control costs and make high profits. Firms can study the variations in quantity supplied with price changes. However, it depends on many factors, such as market conditions and government policies.
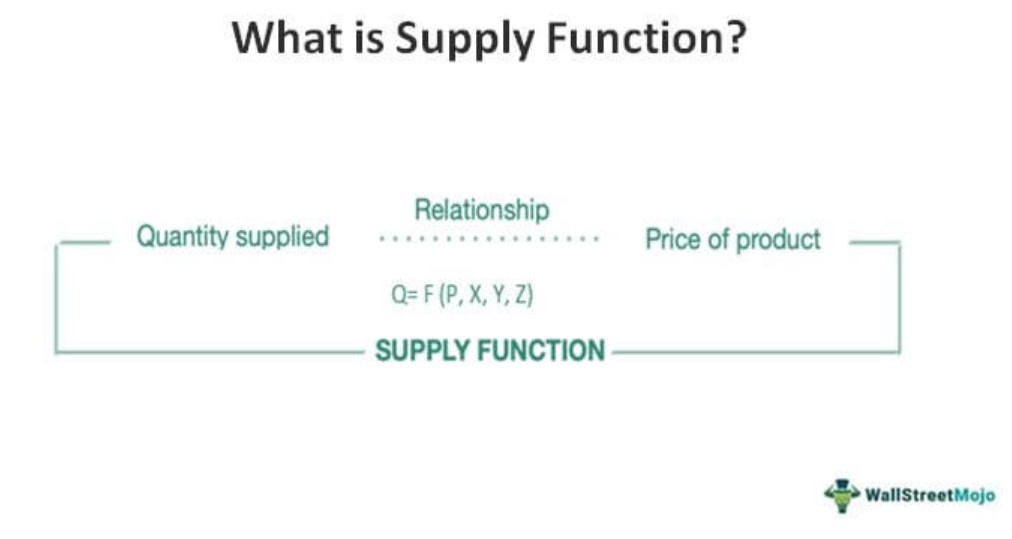
Table of contents
- The supply function is a mathematical equation that expresses the quantity of a commodity supplied as the function of the commodity's price.
- Other factors influencing the function include government policies, wages, raw materials, the technology used, and most importantly, the price of related goods like complimentary items and substitutes.
- The inverse supply function, which depicts the price as a function of quantity, is also an important concept in economics.
- These two functions can help economists, businesses, and governments understand the economy so everyone can benefit from commercial activities.
Supply Function Explained
The supply function formula is as follows:
Qa = f (Pa, Pb , x , y , z)
Here, Qa is the quantity of commodity A supplied
Pa is the price of commodity A
Pb is the price of related commodity B
x, y, and z are other variables affecting the product's supply, like the cost of production, government intervention, level of technology, etc.
Let us look at the various factors affecting supply function in detail.
Firstly, the price of related goods like complementary items and substitutes affects the price of a particular commodity. Consider, for example, a printer that costs $200; if an ink cartridge costs $150, people will not buy the cartridge. Similarly, it is important to take into consideration the competitors' prices. Therefore, a too high or too low price can be both dangerous for a business.
Secondly, the cost of production affects the selling price. This is because the final price is nothing but profit added to the production cost. Therefore, a higher cost will correspond to a higher price. A high cost can directly affect the capacity of a firm to supply. Production cost includes raw materials, wages, and other direct and indirect expenses.
Thirdly, government interventions and policies control the supply level. For example, the government can restrict the amount of a certain commodity that one can supply every month. Lastly, the level of technology affects the speed of supply. Like, advanced production techniques and technology can enable sellers to supply more.
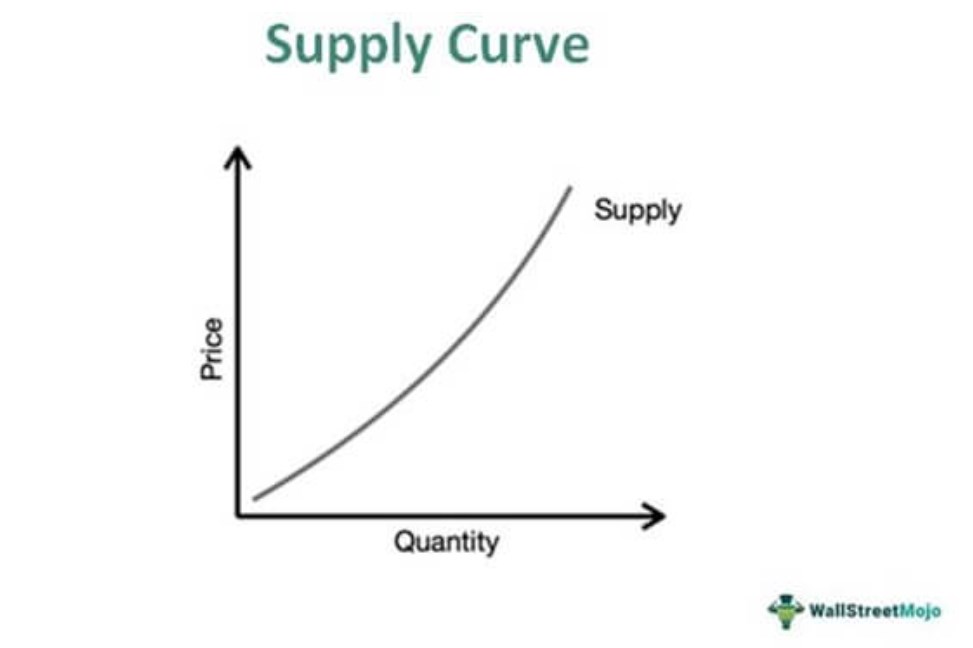
An ideal aggregate supply function can be plotted as a slightly convex line, passing through the origin. This shows that as price increases, supply also increases and vice-versa. That is, if the price of a commodity is high, the seller will be motivated to supply more, as they can earn more from selling high.
Examples
Let's look at the practical examples of this function to understand it better.
Example #1
A firm sells electronic appliances and devices. It defines the supply function for Product A as:
Qa = Pa - 10 Px + 1995.
Px = $200 (average price of substitutes B, C and D)
The firm wants to supply around 200 units every month. Here are the two favorable permutations of quantity and price established by the firm:
(i) Case 1: If the firm wants to supply exactly 200 units
Qa = 200, then solving the equation, Pa = $205
(ii) Case 2: If the firm wants to sell at the average competitors' price, i.e., $200
Pa = $200, then we get Qa = 195
This is a simple example. The function usually varies depending on the firm, commodities, industry, currency, etc.
Example #2
Here's a real-life example. Rising inflation and worsening economic situation worldwide are no news. Especially the prices of commodity items are sky-rocketing. Going by the law of supply, as the price rises, the supply too should increase. However, this doesn't seem to be the case now.
But according to the latest news, supply issues contribute to nearly 50% of the inflation in the United States. A decrease in supply increases the demand, contributing to a rise in prices. However, there is no scope for an increase in supply. The main reasons for this can be attributed to the Russia-Ukraine war. To an extent, the COVID-19-imposed lockdowns are also responsible.
In such cases, businesses can find it challenging to quantify the relationship between prices and quantity supplied.
Inverse Supply Function
The inverse function is the opposite or converse of the direct function of supply. It expresses the price of a certain commodity as a function of the quantity supplied. Hence, its formula would be:
Pa = f ( Qa , x , y , z)
Here Pa is the price of commodity A,
Qa is the quantity supplied
x, y, and z are other variables that affect the function.
Frequently Asked Questions (FAQs)
The supply function formula can help firms establish the relation between price and commodity. The formula can be expressed as:
Q = f ( P)
where Q is the quantity of the product supplied and P is the price.
Firms can define an optimum function based on their requirements. Then, they can use statistical techniques like multiple regression analysis to solve the function.
The aggregate function of supply is a numerical association that helps understand the correlation between the quantity supplied and the price of a commodity. It also considers other variables which influence the supply situation in an economy. Therefore, companies will be able to measure the variation in quantity supplied with varying product prices.
As the term goes, the inverse supply function is contrary to the direct function. In the latter, the quantity supplied is expressed as a function of price, whereas in the inverse function, the price is expressed as a function of quantity. Therefore, the formula goes as follows:
P = f (Q)
where P is price and Q is the quantity supplied.
Recommended Articles
This has been a guide to Supply Function and its meaning. Here we explain its formula, factors affecting it, inverse supply function, and examples. You may learn more from the following articles -
