As we know that standard deviation is a calculation of how the values are changing with comparison or the respect of the mean or the average value, we represent this data in a graph, there are two deviations represented in graph of standard deviation, one which are positive to the mean which is shown on the right hand side of the graph and another is negative to the mean which are shown on the left hand side of the graph, the standard deviation graph is also known as bell curve graph in excel.
Table of Contents
Excel Standard Deviation Graph / Chart
Standard Deviation is one of the important statistical tools which shows how the data is spread out. For example in the stock market how the stock price is volatile in nature.
Typically standard deviation is the variation on either side of the average or means value of the data series values. We can plot the standard deviation in the Excel graph and that graph is called “Bell-Shaped Curve”.
Bell Curve is the graph that is commonly used to gauge the performance appraisal of employees in companies. All the organizations work on performance appraisal for a specific period of time frame, using this performance appraisal they reward employees in terms of salary, promotions, etc.
They gauge employees on Low or Non Performers, Average Performers, and High Performers. When you plot a bell-shaped graph it shows the highest probability of the outcome and probability of the outcome keeps going down when the bell shapes move to either side from the center point.
For example, look at the below Excel bell shapes curve graph.
Assume you are working in a team of 50 members and your rating is very similar to the other team members then only a few employees got a higher rating, a majority will get an average rating and few will get a low rating. If you got 8 as a rating and your team member got 7 as the rating there won’t be much of a difference here, isn’t it??
To make the comparison fair bell-shaped curve best fit to gauge the employee and rate then, reward them accordingly.
All the higher rating employees in the bell curve will be placed on the right-hand side of the bell curve, low rating employees will be placed on the left-hand side of the bell curve, and average employees will be placed in the center of the bell curve.
In order to understand the Excel Standard Deviation Graph or bell-shaped curve, we need two kinds of calculations here. One is MEAN or AVERAGE of the data series, and the second one is Standard Deviation (SD) which shows how to spread out the data series is.
For example, if the average score of the students in the class is 70 and SD is 5 then students scored within either side of the mean value i.e. 70. The first range will be 65-70 and the second range will be 70-75.
How to Create a Standard Deviation Graph (Chart) in Excel?
For a better understanding of the Standard Deviation Graph (Chart) in Excel, let’s consider our real-life example of student’s marks in an examination.
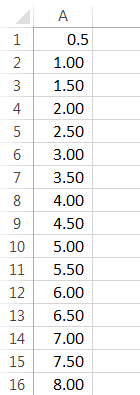
I have taken 25 students sample data and below are the scores of these 25 students in an examination.
The first thing we need to do is calculate the AVERAGE score of the examination. Apply the Average Formula.
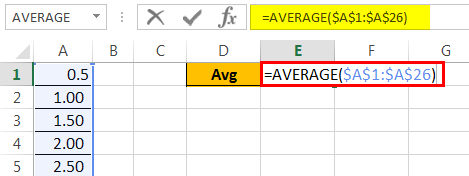
we got the result as 7.
Secondly, calculate the Standard Deviation of the data series.
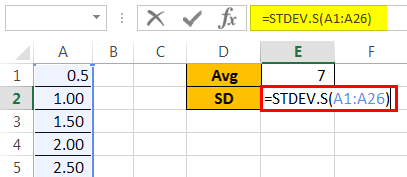
The result is shown below:
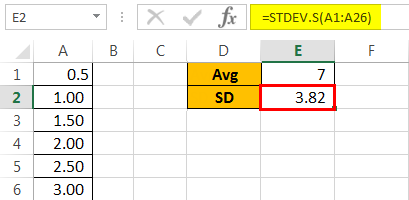
Note: Since I had taken sample data, I have used STDEV.S, which is used for sample data series.
Now in the B1 cell enter normal distribution excel formula i.e. NORM.DIST.
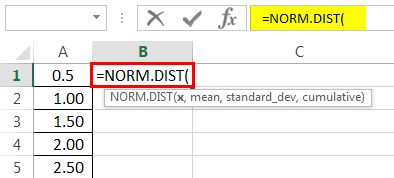
x is nothing but our data point, so select A1 cell.
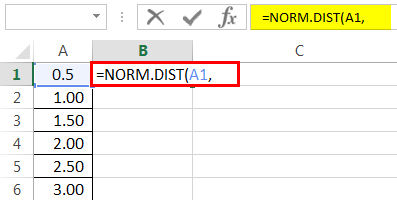
MEAN is the average value we have calculated so give a link to the cell E1 and make it an absolute reference.
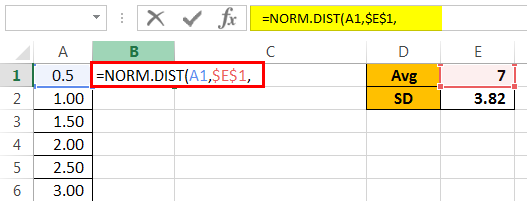
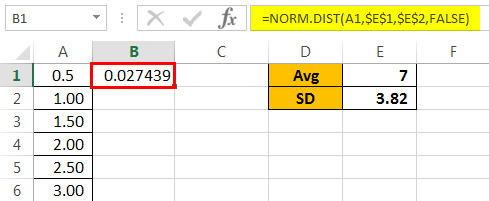
Next is SD to give a link to the cell E2 and make it absolute excel reference.
Next thing is Cumulative, select FALSE as the argument.
Now see the result.
Drag the formula to other cells to have normal distribution values.
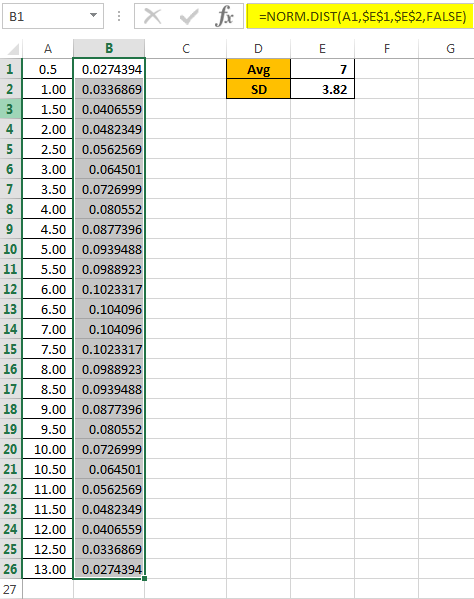
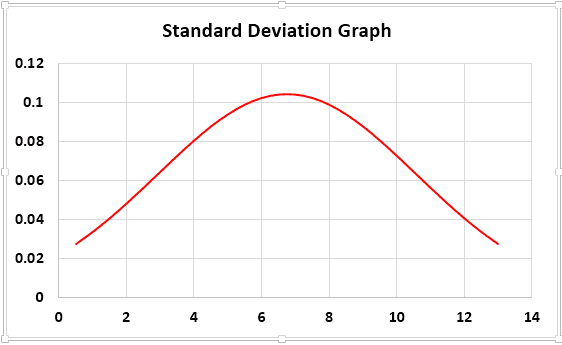
Create a Standard Deviation Excel graph using below steps:
Step 1: Select the data and go to the INSERT tab then, under charts select scattered chart then, select Smoother Scatter Chart.
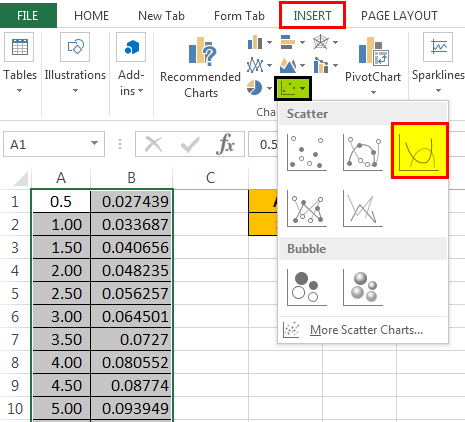
Step 2: Now we will have a chart like this.
Step 3: If needed you can change the chart axis and title.
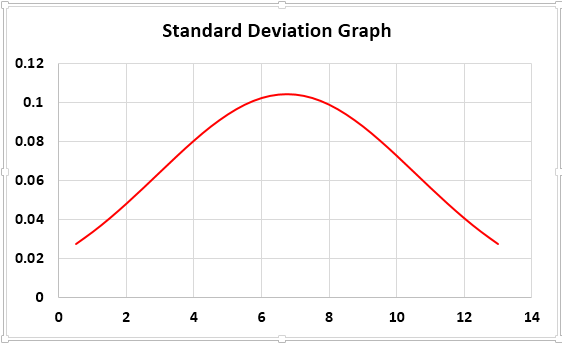
Conclusion: Our SD is 3.82 which is slightly higher so our bell curve is wider. If the SD is small then we will get a slim bell curve.
Things to Remember About Standard Deviation Graph in Excel
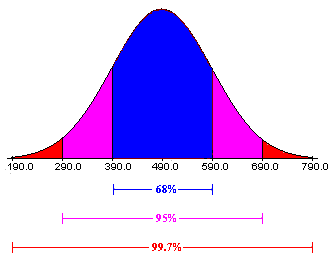
- MEAN or AVG values are always the center point of the Excel Standard Deviation graph.
- Approximately 68.2% of the data series will be fitted in the range i.e. MEAN – SD to MEAN + SD. (65-70)
- Approximately 95.5% of the data series will be fitted in the range i.e. 2 * (MEAN –SD) + 2 * (MEAN + SD).
- Approximately 99.7% of the data series will be fitted in the range i.e. 3 * (MEAN –SD) + 3 * (MEAN + SD).
- Excel Standard Deviation Graph shape depends on the SD value, higher the SD value wide the bell curve, and smaller the SD value, slimmer the bell curve is.
- Complete knowledge of the bell curve can be best explained by the statistical person and I am limited to the excel sheet.
Standard Deviation Graph in Excel Video
Recommended Articles
This has been a guide to the Standard Deviation Graph in Excel. Here we discuss how to create a Standard Deviation Chart / Graph in Excel along with practical examples and downloadable excel template. You may learn more about excel from the following articles –
- Formula of Sample Standard Deviation
- Excel Normal Distribution Graph
- How to Make a Graph in Excel?
- How to Create a Gantt Chart in Excel
- 35+ Courses
- 120+ Hours
- Full Lifetime Access
- Certificate of Completion
