Skewness

Skewness describes how much statistical data distribution is asymmetrical from the normal distribution, where distribution is equally divided on each side. If a distribution is not symmetrical or normal, it is skewed, i.e., the frequency distribution is skewed to the left or right. A skewness distribution is usually depicted through a bell curve on a graph.

It tells the analyst or an investor about the direction of outliers within the distribution. In a negative skew, the tail of the distribution curve is elongated on the left side. It means that the outliers are further in towards the left and farther from the mean. Therefore, it shows the symmetry or asymmetry within the distribution.

• Skewness demonstrates how the normal distribution of statistical data, which is symmetrical on both sides, differs from reality. 
• Consider a distribution that is skewed, neither symmetrical nor regular. It denotes a left- or right-skewed frequency distribution.
• Skewness can be either positive or destructive.
• It displays how far the data set strays from the expected distribution. The data set indicates that a substantial negative number negatively skews the distribution. The data set also contains a vast positive value, suggesting favorable distribution. Additionally, it is a superb statistical tool for forecasting investor distribution returns.

Skewness is the measurement of symmetry or asymmetry within a distribution. It shows the outliers in the distribution and their direction. It is usually caused by a heavily condensed activity within one range and less so in the other range.

Positive and negative skewness is usually found while analyzing data sets because situations usually have data points from both extremes of the spectrum and the asymmetric distribution causes skewness to be a part of the analysis.

Skewness is how much the data set deviates from its normal distribution. A larger negative value in the data set means the distribution is negatively skewed, and a larger positive value in the data set means the distribution is positive. It is a good statistical measure that helps the investor predict distribution returns.

Statistics play an important role when the data distribution is not normal. The extreme data points in the data set can lead data distribution to skew towards the left (extreme data in the data set are smaller, which skew the data set negative, which results mean<median<mode ) or to skew towards the right (i.e., extreme data are larger, that skew data set positive which results mean>median>mode). It helps an investor with a short-term holding period to analyze the data to identify the trend falling at the end of the distribution.

Let us understand the different types based on negative or positive skewness within the distribution through the discussion below.

If the distribution is symmetric, it has a skewness of 0 and its Mean = Median = Mode.

So basically, there are two types:

• Positive: The distribution is positively skewed when most of the distribution frequency lies on the right side and has a longer and fatter right tail where the distribution’s Mean > median > Mode.

• Negative: The distribution is negatively skewed when most of the distribution frequency lies on the left side and has a longer and fatter left tail. Where the distribution’s Mean < Median < Mode.

Before discussing the concept of skewness distribution any further, it is important we understand the formula to calculate points to plot in the graph. This will help us understand the intricate details of the concept which will be discussed further in the article.

The Skewness formula is represented below -

There are several ways to calculate the skewness of the data distribution. One of which is Pearson’s first and second coefficients.

• Pearson’s first coefficients (mode Skewness): It is on the Mean, mode, and standard deviation.

Formula: (Mean – Mode)/Standard Deviation.

• Pearson’s second coefficient (median skewness): It is on the distribution's mean, median, and standard deviation.

 Formula: (Mean – Median)/Standard Deviation.

As you can see above, Pearson’s first coefficient of skewness has a mode as its one variable to calculate it. It is useful when data has a more repetitive number in the data set. However, suppose only a few repetitive data in the data set belong to mode. In that case, Pearson’s second coefficient of skewness is a more reliable measure of central tendency as it considers the median of the data set instead of the mode.

For example:

Data set (a):  7,8,9,4,5,6,1,2,2,3.

Data set (b):  7,8,4,5,6,1,2,2,2,2,2,2,2,2,2,2,3.

For both the data sets, we can conclude the mode is 2. But it does not make sense to use Pearson’s first coefficient of skewness for data set(a) as its number 2 appears only twice in the data set, but one can use it to make for data set(b) as it has a more repetitive mode.

Another way to calculate skewness is by using the below formula:

• = Random variable.
• X = Distribution Mean.
• N = Total variable in the distribution.
• α = Standard Deviation.

Let us take the help of an example to understand positive and negative skewness in depth.
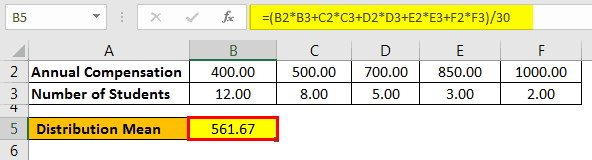
In XYZ management college, 30 final-year students are considering job placement into the QPR research firm & their compensations are based on the student’s academic performance and past work experience. Below is the student’s compensation data in the PQR research firm.

Solution

Use the below data:

Calculation of Distribution Mean 

• = ($400*12+$500*8+$700*5+$850*3+$1000*2)/30
• Distribution Mean = 561.67

Calculation of Standard Deviation

• Standard Deviation= √{(Sum of the deviation square * No. of students)/N}.
• Standard Deviation = 189.16

Calculation of Skewness can be done as follows -

• Skewness: (sum of the Deviation Cube)/(N-1) * Standard deviation’s Cube.
• = (106374650.07) / (29 * 6768161.24)
• = 0.54

Hence, the value of 0.54 tells us that the distribution data skew from the normal distribution.

Let us discuss the advantages of negative and positive skewness through the discussion below.

• Skewness is better for measuring the performance of investment returns.
• The investor uses it when analyzing the data set as it considers the extreme of the distribution.
• It is a widely used tool in statistics as it helps understand how much data is asymmetry from the normal distribution.

Despite the various advantages of the skewness distribution as discussed above, there are a few disadvantages that make using this statistical tool a hassle. Let us cover all bases of the concept through the points below.

• Skewness ranges from negative to positive infinity. Sometimes, it is difficult for an investor to predict the trend in the data set.
• An analyst is forecasting the future performance of an asset using the financial model, which usually assumes that data is normally distributed. But, if the data distribution skews, this model will not reflect the actual result in its assumption.

This article has been a guide to Skewness and its meaning. Here we explain its formula, how to calculate, types, and examples, with advantages, and disadvantages. You may also have a look at the following articles: -

• Normal Distribution in Statistics
• Mode in Excel
• Calculate Standard Error
• Poisson Distribution Excel