Sensitivity And Specificity

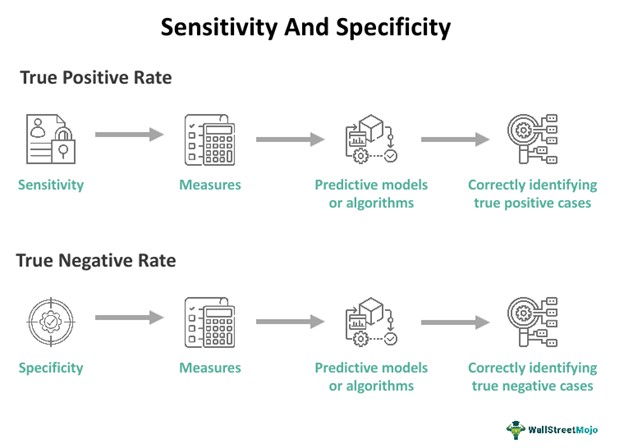
Sensitivity is a statistical measure that gauges a test or model's ability to correctly identify positive cases, while specificity measures its ability to identify negative cases accurately. These metrics are fundamental in assessing the reliability of diagnostic tests and classification models, guiding decision-making in various domains.

The significance of sensitivity and specificity lies in their crucial roles in evaluating the performance of diagnostic tests and classification models. Both these measures profoundly influence decision-making in various domains. They quantify the accuracy, reliability, and trade-offs associated with diagnostic tests and classification models, ultimately shaping treatment decisions, public health strategies, and more.

• Sensitivity measures a test's ability to correctly identify true positive cases, while specificity assesses its ability to identify true negative cases correctly. These metrics are vital in evaluating the performance of diagnostic tests, classifiers, and quality control processes.
• In addition to sensitivity and specificity, precision and recall are used in classification problems. Precision focuses on the proportion of true positives among predicted positives, while recall emphasizes the ability to detect true positives.
• The choice between high sensitivity and high specificity depends on the specific context and the associated costs of false positives and false negatives. A trade-off often exists where increasing one measure can decrease the other.

In statistics, sensitivity (true positive rate) measures the ability to correctly identify
true positive cases, while specificity (true negative rate) measures the
ability to correctly identify true negative cases in a binary classification
test or model.

Sensitivity represents the percentage of true positives, measuring the test's ability to identify individuals with the target condition accurately. However, it does not reflect the proportion of people with the condition who will test positive. Rather, it signifies the proportion of those with the condition who are correctly identified as having it by the test.

Specificity, on the other hand, signifies the percentage of true negatives, indicating the test's ability to identify individuals without the target condition correctly. Similarly, it does not represent the proportion of condition-free individuals who will test negative. Instead, it signifies the proportion of those without the condition who are correctly identified as not having it by the test.

In statistical terms, sensitivity and specificity are calculated as follows:

Sensitivity = True Positives / (True Positives + False Negatives)

Specificity = True Negatives / (True Negatives + False Positives)

Both these measures are essential in determining how accurately a test identifies positive and negative cases and in assessing the overall performance and reliability of the test or model.

To help remember the distinctions between sensitivity and specificity, two mnemonics are often used:

1. SnNout: When a test has high sensitivity (Sn) and the result is negative (N), it's valuable for ruling out a disease or condition (out). This means that a highly sensitive test, when negative, helps exclude the possibility of the disease being present.
2. SpPin: Conversely, when a test has high specificity (Sp) and the result is positive (P), it's useful for confirming or ruling in the presence of a disease (in). In this context, a test with high specificity, when positive, indicates the likelihood of the disease being present.

Some of the examples are the following:

Example #1

Let us assume a security scanner at an airport. It's engineered to spot weapons (true positives) while ensuring innocent passengers aren't mistakenly flagged for harmless items (false positives). The scanner detects 90% of concealed weapons (high sensitivity) and only gives false alarms for 5% of passengers without weapons (high specificity). This means it effectively catches most threats without causing unnecessary delays for innocent travelers.

Example #2 - Quality Control in Manufacturing

Consider a quality control test in manufacturing aimed at identifying defects in products. A test with high sensitivity would effectively catch most of the actual defects in the products, reducing the likelihood of false negatives. This ensures that most faulty items are detected, preventing them from reaching consumers and maintaining product quality.

Conversely, high specificity in the quality control test would minimize false alarms by correctly identifying defect-free products. This reduces unnecessary rework and waste in the production process, saving time and resources while maintaining confidence in the product's quality.

Sensitivity and specificity are critically important concepts in various fields, especially in healthcare, diagnostics, quality control, and risk assessment. They serve distinct yet complementary roles in evaluating the performance and reliability of tests, models, and screening processes.

The balance between sensitivity and specificity is context-dependent and should be tailored to the specific goals and consequences of the test. Depending on the application, one measure may be prioritized, or adjustments may be made to achieve the desired balance. The combined assessment of sensitivity and specificity provides a comprehensive view of a test's performance, guiding decision-making processes in various domains, ultimately leading to more accurate diagnoses, better quality control, and reduced risks.

When evaluating the performance of classification models, it's essential to understand the differences between sensitivity and specificity on one hand and precision and recall on the other.

#1 - Sensitivity (True Positive Rate, TPR) And Specificity (True Negative Rate, TNR)

Sensitivity measures the proportion of actual positive cases correctly identified by a classifier. It assesses how well the model detects positive cases, and high sensitivity is vital when missing true positives has serious consequences.

Formula: Sensitivity = True Positives / (True Positives + False Negatives)

Specificity measures the proportion of actual negative cases correctly identified by a classifier. It evaluates the model's ability to avoid false alarms (false positives), which is crucial when the cost of false positives is significant.

Formula: Specificity = True Negatives / (True Negatives + False Positives)

#2 - Precision And Recall (Sensitivity, True Positive Rate)

Precision is the proportion of predicted positive cases that are actually true positives. It assesses how well the model avoids false alarms, meaning that when the model predicts a positive case, it is highly likely to be correct.

Formula: Precision = True Positives / (True Positives + False Positives)

Recall (also known as Sensitivity) measures the proportion of actual positive cases correctly identified by a classifier. It quantifies how well the model detects positive cases and implies a lower likelihood of missing true positive cases.

Formula: Recall = True Positives / (True Positives + False Negatives)

This article has been a guide to Sensitivity and Specificity and its definition. We explain its formula, examples, comparison with precision & recall, and importance. You may also find some useful articles here -

• ROC Curve
• Mahalanobis Distance
• Quantitative Risk Analysis