Sampling Distribution

Sampling distribution in statistics refers to studying many random samples collected from a given population based on a specific attribute. The results obtained provide a clear picture of variations in the probability of the outcomes derived. As a result, the analysts remain aware of the results beforehand, and hence, they can make preparations to take action accordingly.

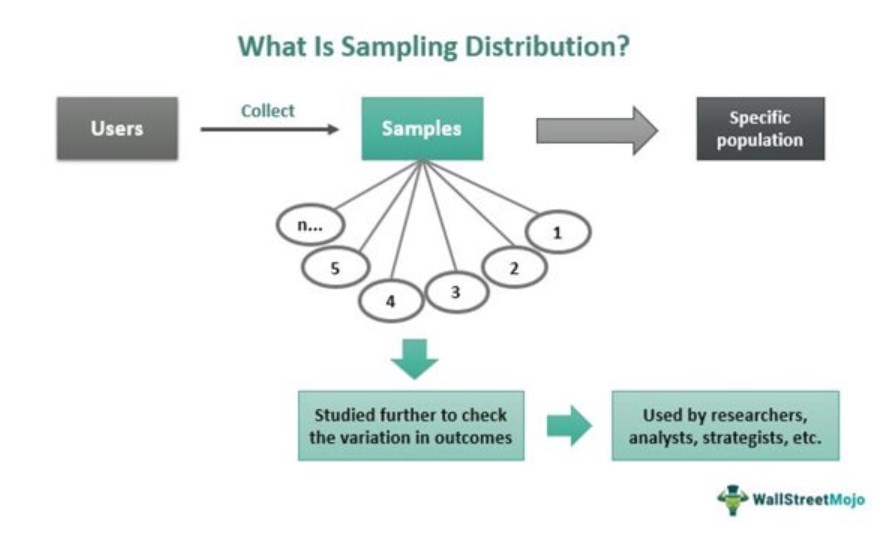
As the data is based on one population at a time, the information gathered is easy to manage and is more reliable as far as obtaining accurate results is concerned. Therefore, the sampling distribution is an effective tool in helping researchers, academicians, financial analysts, market strategists, and others make well-informed and wise decisions.

• Sampling distribution refers to studying the randomly chosen samples to understand the variations in the outcome expected to be derived.
• Many researchers, academicians, market strategists, etc., go ahead with it instead of choosing the entire population.
• Sampling distribution of the mean, sampling distribution of proportion, and T-distribution are three major types of finite-sample distribution.
• The central limit theorem states how the distribution still remains normal and almost accurate with increasing sample size.

Sampling distribution in statistics represents the probability of varied outcomes when a study is conducted. It is also known as finite-sample distribution. In the process, users collect samples randomly but from one chosen population. A population is a group of people having the same attribute used for random sample collection in terms of statistics. 

However, the data collected is not based on the population but on samples collected from a specific population to be studied. Thus, a sample becomes a subset of the chosen population. With sampling distribution, the samples are studied to determine the probability of various outcomes occurring with respect to certain events. For example, deriving data to understand the adverts that can help attract teenagers would require selecting a population of those aged between 13 and 19 only.

Using finite-sample distribution, users can calculate the mean, range, standard deviation, mean absolute value of the deviation, variance, and unbiased estimate of the variance of the sample. No matter for what purpose users wish to use the collected data, it helps strategists, statisticians, academicians, and financial analysts make necessary preparations and take relevant actions with respect to the expected outcome.

As soon as users decide to utilize the data for further calculation, the next step is to develop a frequency distribution with respect to individual sample statistics as calculated through the mean, variance, and other methods. Next, they plot the frequency distribution for each of them on a graph to represent the variation in the outcome. This representation is indicated on the distribution graph.

Moreover, the accuracy of the distribution depends on various factors, and the major ones that influence the results include:

• Number of observations in the population. It is denoted by “N.”
• Number of observations in the sample. It is denoted by “n.”
• Methods adopted for choosing samples randomly. It leads to variation in the outcome.

The finite-sample distribution can be expressed in various forms. Here is a list of some of its types:

#1 - Sampling Distribution of Mean

It is the probabilistic spread of all the means of samples of fixed size that users choose randomly from a particular population. When they plot individual means on the graph, it indicates normal distribution. However, the center of the graph is the mean of the finite-sample distribution, which is also the mean of that population.

#2 - Sampling Distribution of Proportion

This type of finite-sample distribution identifies the proportions of the population. The users select samples and calculate the sample proportion. They, then, plot the resulting figures on the graph. The mean of the sample proportions gathered from each sample group signifies the mean proportion of the population as a whole. For example, a Vlogger collects data from a sample group to find out the proportion of it interested in watching its upcoming videos.

#3 - T-Distribution

People use this type of distribution when they are not well aware of the chosen population or when the sample size is very small. This symmetrical form of distribution fulfills the condition of standard normal variate. As the sample size increases, even T distribution tends to become very close to normal distribution. Users use it to find out the mean of the population, statistical differences, etc.

This type of distribution plays a vital role in ensuring the outcome derived accurately represents the entire population. However, reading or observing each individual in a population is difficult. Therefore, selecting samples from the population randomly is an attempt to make sure the study conducted could help understand the reactions, responses, grievances, or aspirations of a chosen population in the most effective way.

The method simplifies the path to statistical inference. Moreover, it allows analytical considerations to focus on a static distribution rather than the mixed probabilistic spread of each chosen sample unit. This distribution eliminates the variability present in the statistic.

It provides us with an answer about the probable outcomes which are most likely to happen. In addition, it plays a key role in inferential statistics and makes almost accurate inferences through chosen samples representing the population.

Let us consider the following examples to understand the concept better:

Example #1

Sarah wants to analyze the number of teens riding a bicycle between two regions of 13-18.

Instead of considering each individual in the population of 13-18 years of age in the two regions, she selected 200 samples randomly from each area.

Here,

• The average count of the bicycle usage here is the sample mean. 
• Each chosen sample has its own generated mean, and the distribution for the average mean is the sample distribution. 
• The deviation obtained is termed the standard error.

She plots the data gathered from the sample on a graph to get a clear view of the finite-sample distribution.

Example #2

Researcher Samuel conducts a study to determine the average weight of 12-year-olds from five different regions. Thus, he decides to collect 20 samples from each region. Firstly, the researcher collects 20 samples from region A and finds out the mean of those samples. Then, he repeats the same for regions B, C, D, and E to get a separate representation for each sample population.

The researcher computes the mean of the finite-sample distribution after finding the respective average weight of 12-year-olds. In addition, he also calculates the standard deviation of sampling distribution and variance. 

The discussion on sampling distribution is incomplete without the mention of the central limit theorem, which states that the shape of the distribution will depend on the size of the sample. 

According to this theorem, the increase in the sample size will reduce the chances of standard error, thereby keeping the distribution normal. When users plot the data on a graph, the shape will be close to the bell-curve shape. In short, the more sample groups one studies, the better and more normal is the result/representation.

This is a guide to what is Sampling Distribution & its definition. We explain its types (mean, proportion, t-distribution) with examples & importance.. You can learn more about from the following articles -

• Attribute Sampling
• Stratified Sampling
• Central Limit Theorem
• Statistics in Excel