Sample Standard Deviation Formula

Publication Date :

26 Jun, 2023

Blog Author :

Edited by :

Reviewed by :

Download FREE Sample Standard Deviation Formula Excel Template and Follow Along!

Sample Standard Deviation Formula Excel Template.xlsx

Table Of Contents

What Is The Sample Standard Deviation Formula?

Sample standard deviation refers to the statistical metric used to measure the extent to which a random variable diverges from the sample’s mean. One may calculate it by adding the squares of the deviation of each variable from the mean, dividing the result by several variables minus, and computing the square root in Excel of the result.

Formula of Sample Standard deviation

The sample standard deviation formula for grouped data helps statisticians to study a population more accurately by understanding the chances of diversion from the standard results that are obtained during the research.

Key Takeaways

Sample standard deviation is the statistical tool used to determine the extent to which a random variable diverges from the sample's mean.
One may calculate it by adding the squares of the deviation of each variable from the mean, dividing the result by several variables minus, and computing the square root in Excel of the result.
The concept of sample standard deviation is essential from a statistician's point of view since sample data typically comes from a large variable pool (population)
from which the statistician anticipates calculating or generalizing the results for the entire population.

Sample Standard Deviation Formula Explained

The standard deviation formula for sample helps calculate the figures that let researchers know the chances of deviations in the results obtained through a study with respect to a population. It is a measure in the field of statistics and commonly used in innumerable areas of scientific study where there is a need to quantify the amount from within a sample data. It gives important information about the spread of the points around the mean. This increases the clarity and dependability of the decisions taken and analysis made in various fields.

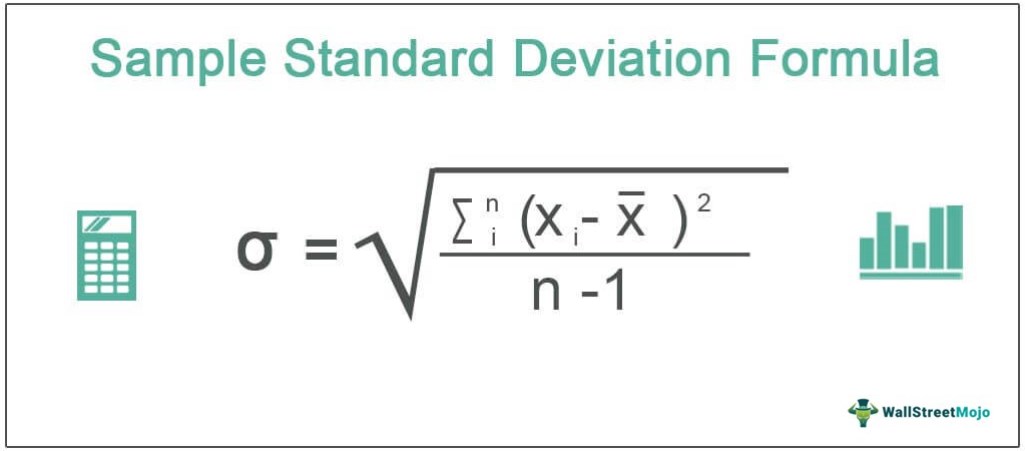
The mathematical expression

σ = √ ∑_iⁿ (xi - X)² / (n-1)

where

x_i = i^th random variable
X = Mean of the sample
n = number of variables in the sample

Therefore, given above is the basic formula for calculation of standard deviation. The meaning of each variable in the standard deviation formula for sample is explained.

How To Calculate?

There is a series of steps that help find out the deviations using the formula of sample standard deviation: Let us have a look at them:

Firstly, gather random variables from a population of a large number of variables. These variables will form a sample. The variables are denoted by xi.
Next, determine the number of variables in the sample, and denote by n.
Next, determine the sample's mean by adding all the random variables and dividing the result by the number of variables in the sample. The sample mean is denoted by x.
Next, compute the difference between each variable of the sample and the sample mean, i.e., x_i – x.
Next, calculate the square of all the deviations, i.e. (x_i – x)².
Next, add all the squared deviations, i.e. ∑ (xi – x)².
Next, divide the summation of all the squared deviations by the number of variables in the sample minus one, i.e. (n – 1).
Finally, the formula for sample standard deviation is calculated by computing the result's square root, as shown below.

The above steps give a detailed description of how to use the formula of sample standard deviation for calculating deviation of some sample data after collecting them form a large data set.

Examples

Let us consider the following examples of sample standard deviation formula usage:

Example #1

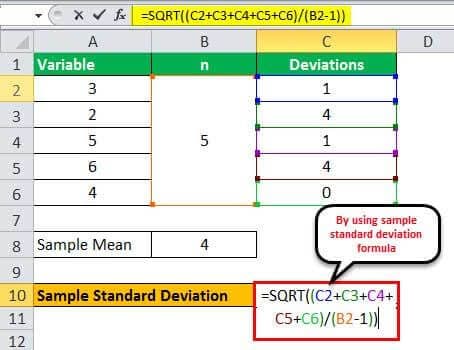
Let us take the example of a sample of 5 students surveyed to see how many pencils they were using every week. Then, calculate the sample standard deviation based on their given responses: 3, 2, 5, 6, and 4.

Given,

Sample size (n) = 5

Below is given data for the calculation of sample standard deviation.

Sample Mean

The calculation of the sample mean:

Sample mean = (3 + 2 + 5 + 6 + 4) / 5

Sample Mean = 4

One can calculate the squares of the deviations of each variable as below,

(3 – 4)² = 1
(2 – 4)² = 4
(5 – 4)² = 1
(6 – 4)² = 4
(4 – 4)² = 0

Now, one can calculate the deviation using the sample standard deviation formula example in Excel as shown below:

ơ = √ {(1 + 4 + 1 + 4 + 0) / (5 – 1)}

Deviation will be -

Sample Standard deviation formula example1.3jpg

ơ = 1.58

Therefore, the sample standard deviation is 1.58.

Example #2

Let us take the sample standard deviation formula example of an office in New York where around 5,000 people work, and a survey has been carried out on a sample of 10 people to determine the average age of the working population. But, first, determine the sample standard deviation based on the ages of the 10 people: 23, 27, 33, 28, 21, 24, 36, 32, 29, and 25.

Given,

Sample size(n) = 10

Sample Standard deviation formula example2

By using the above data, we will first calculate the sample mean:

Sample Mean

The calculation of sample mean:

= (23 + 27 + 33 + 28 + 21 + 24 + 36 + 32 + 29 + 25) / 10

Sample Standard deviation formula example2.1

Sample Mean = 27.8

One can calculate the squares of the deviations of each variable as below:

(23 – 27.8)² = 23.04
(27 – 27.8)² = 0.64
(33 – 27.8)² = 27.04
(28 – 27.8)² = 0.04
(21 – 27.8)² = 46.24
(24 – 27.8)² = 14.44
(36 – 27.8)² = 67.24
(32 – 27.8)² = 17.64
(29 – 27.8)² = 1.44
(25 – 27.8)² = 7.84

Deviation

Now, the deviation can be calculated by using the above formula as,

ơ = √ {(23.04 + 0.64 + 27.04 + 0.04 + 46.24 +14.44 +67.24 + 17.64 + 1.44 + 7.84) / (10 – 1)}

Deviation will be -

Sample Standard deviation formula example2.3jpg

ơ = 4.78

Referring to the Excel sheet above to understand the detailed calculation.

Therefore the above examples give us a clear idea about the process of using the sample standard deviation formula statistics and the results that can be derived from it.

Relevance and Uses

Let us look at some of the uses of the formula.

The concept of sample standard deviation is very important from a statistician's perspective because a sample of data usually takes from a pool of large variables (population) from which the statistician expects to estimate or generalize the results for the entire population. The measure of standard deviation is no exception to this. Hence, the statistician has to assess the population standard deviation based on the sample drawn, and that is where such deviation comes into play.

It helps understand the dataset’s variability or diversity from where the sample is drawn. This helps compare the data drawn from different populations or samples. If two datasets are taken and sample is drawn from them, the set with higher standard deviation will have higher variability.
The formula helps identify the outliers, which are the points far away from the mean.
The sample standard deviation formula statistics identifies and evaluates the stability and consistency of the process or operation. This is used in manufacturing and quality control by pointing out the variations and defects in a sample dataset. This, in turn, indicates a requirement for process improvement and control.
It is also used to assess the risk or a portfolio while making any investment because the formula helps in analysing the volatility of the investment opportunity. Investors can compare the risk and return and take investment decisions accordingly and financial advisors can design portfolios for their clients which will give maximum return at minimum risk.

Thus the above are some of the uses of the formula in the financial market.