Table Of Contents
What Is Rule Of 69?
Rule of 69 is a general rule to estimate the time that is required to make the investment to be doubled, keeping the interest rate as a continuous compounding interest rate, i.e., the interest rate is compounding every moment. It does not provide the exact time but very close to proximity without using the pure mathematical formula.
This method gives an estimate that approximates the period needed for doubling the money. It is widely used since it involves an easy calculation. The concept has variations like the Rule of 72, which is commonly used in case of low returns. However, using this concept, the investor can very quickly decide the investment's viability without complex calculations.
Table of contents
- The Rule of 69 states that when a quantity grows at a constant annual rate, it will roughly double in size after approximately 69 divided by the growth rate.
- The Rule of 69 is derived from the mathematical constant e, which is the base of the natural logarithm. The natural logarithm of 2 is approximately 0.693, and thus, the value 69 is used as an approximation.
- The Rule of 69 finds widespread application in various fields, including finance, economics, population studies, and other disciplines. It provides a quick estimation of doubling times and aids in understanding the speed of growth or compounding.
Rule Of 69 Explained
The rule of 69 is a method widely used to calculate how long it will take for the invested amount to get doubled in value. The calculation does not give an accurate answer, but rather just an estimate of time. Therefore rule of 69 in finance is suitable to get an idea, and not for final decision making, especially if the investment involves a huge sum of money.
It is better to understand first that before applying rule 69, check whether the security or case on which we are applying the model is compound on a regular basis or have a different pattern. There is a category between 69 to 72 for the denominator part. As the continuous compounding decrease to become normal compounding, we shift from rule 69 to rule 72.
It can be said that the time required to make the investment double is inversely proportionate to the interest rate, so if the interest rate is increased, then there will be less time required to make it double. It should always be kept in mind that the answer provides hereby is not the exact answer, so it needs to cover only the cases where the just a normal side by the figure requires not the exact time.
It is used only for the financial items which are using the continuous compounding interest rate as the compounding form, So not applicable generally on loan given by banks to the customer (Compound interest is applied in that case) or unsecured loan is given or taken from others. (Simple interest is applied).
This formula works only in the condition where the interest rate does not change in between, i.e., a similar rate throughout the period; otherwise, the result can deviate from the result obtained using this rule.
People are concerned with the investment horizon only if the amount involved herewith is huge in size. If required dedicated complexity calculative sheet to determine so not reliable for those projects, and even the little change in a variable can have a serious impact on deciding whether to do the project or not, so not worthy of using it.
Formula
It is important to understand the formula that is used for calculation of the same which is as given below.

Type Of Rules
Types of rules for calculating the no. of years take to make the investment double.
- Rule of 72: It is used for the simple compound rate of interest.
- Rule of 70: It is used when the interest rate for the financial product is of a compounding nature, not of continuous compounding.
- Rule of 69: It is used when the interest rate is given is continuous compounding.
Examples
Below are some of the examples of the rule of 69.
Example #1
If an amount of $1 Mn is invested at the rate of 10%, then how much time will it take to make our investment to become $2Mn
Solution:
Calculation of doubling period will be -
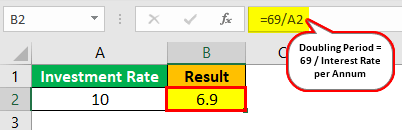
Doubling Period = 69/10
Doubling Period = 6.9 Years.
Consider the same example; if the ask was how much time it will take to become 8 Mn, then we consider simple find it as
| Initial Money | Rate of Int | At the End | Time |
|---|---|---|---|
| 100 | 10 | 200 | 6.9 |
| 200 | 10 | 400 | 13.8 |
| 400 | 10 | 800 | 27.6 |
| 800 | 10 | 1,600 | 55.2 |
| 1,600 | 10 | 3,200 | 110.4 |
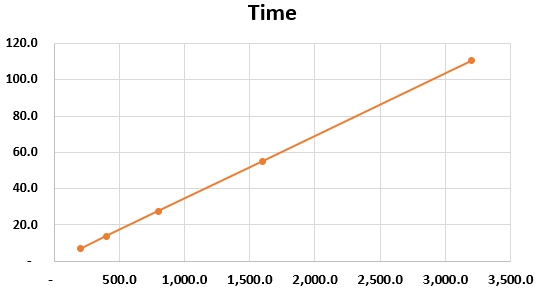
The total time will be 27.6 Years.
Example #2
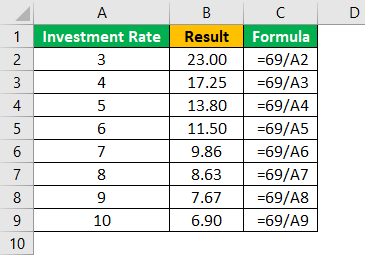
If there is a security whose compounding rate of Int. is as follows, determine the time required to make it double.
Solution:
Calculation of doubling period will be -
Benefits
The following are the benefits of the rule of 69.
- It assumes that the interest is continuously compounding. In fact, it is true to think in the case of equity valuation that is compounding on an instant basis.
- It provides the answer very close to the answer obtained by using a financial calculator.
- Rule of 69 in finance is even considered as the thumb rule of the investment return generating a cycle.
- Easy to calculate the time required.
- Even the retail investor or a non-finance person can easily determine the result.
- Can be used by any person without understanding the pure logic.
- Faster decision making and improve thought process.
Limitations
The following are the limitations of the rule of 69.
- Difficult to explain the logic behind the number 69.
- Rule 69 does not apply to everything. Only the security like equity, which is compounding every minute, can provide the exact value (Rule 72 can Be help in those cases)
- If the rate is too less like 2/3 % Per annum, than the result of of rule of 69 formula is not very accurate. Generally, the higher rate is well captured by this formula.
- Projects with a heavy investment need specially designed spreadsheets because a minuscule difference in time and rate of interest value can create a difference of millions.
- Difficult to absorb the value derived because of non-transparency of value derivation.
- This rule covers those instruments which compounds continuously like equity shares, but it ignores the dividend component which is also received by the equity holder, so overall the share did not increase by an exact multiple of 2, but the dividend amount makes the value of it.
Thus, the above are some essential benefits and limitations listed clearly, which investors should keep in mind while using the method. After going through all the details, it can be concluded that this kind of calculation simple provides a quick and easy way to forecast or estimate the doubling time if we invest an amount in any kind of fixed return option. In real life scenarios, it does not always work.
Rule Of 69 Vs Rule Of 72
Both the above are used by investors to calculate or estimate the possible time period within which the investment amount will increase. But there are some differences between them as follows:
- The former is used for any rate of interest whereas the latter is used mainly in case the interest is non-continuous.
- In case the rate of interest is increasing then the former will give a more precise or clearer answer than the latter.
Thus, even though both the concepts amy appear to be similar in nature, there are some differences as give above. But both are equally important and useful and are commonly used by accountants and financial planners who deal with investment decisions.
Frequently Asked Questions (FAQs)
The Rule of 69 is an approximation that works well for growth rates that are relatively small or moderate. However, as the growth rate increases or approaches extreme values, the accuracy of the rule diminishes.
The Rule of 69 can be used for positive and negative growth rates, although the interpretation may differ. For example, the rule estimates the doubling time for positive growth rates while it estimates the halving time for negative growth rates. In both cases, the Rule of 69 provides a convenient approximation to understand the rate of change over time.
The Rule of 69 is closely related to exponential growth. Exponential growth refers to a process where a quantity increases at a constant percentage rate over equal time intervals. The Rule of 69 allows us to estimate the doubling time for quantities exhibiting exponential growth. In exponential growth, the time it takes for the quantity to double remains relatively constant, and the Rule of 69 provides a quick way to approximate this doubling time.
Recommended Articles
This has been a guide to what is Rule Of 69. We explain the formula along with differences with rule of 72 the benefits, limitations & types of rules. You can learn more about accounting from the following articles –
