Root Mean Square

Last Updated :

Blog Author :

Edited by :

Reviewed by :

Table Of Contents

What Is Root Mean Square?

Root Mean Square (RMS) is the square root of mean square, which is the arithmetic mean of the squares of a set of values. It is another name for the quadratic mean. It is a particular case of the generalized mean, whose exponent is 2.

The calculating magnitude of a group of numbers is the difference between the two sets of data. Due to the importance of bigger variances, the root mean square value is more frequently used than the arithmetic average. It is mostly used to calculate several values' root mean square deviation.

What is Root Mean Square?

The root mean square formula provides the square root of each data point's entire sum of squares in an observation.
The square root of the arithmetic mean of the squares of a group of values is their root mean square. It is also known as the quadratic mean.
Its value is greater than or equal to the average number of terms.
It has a lot of applications in various scientific, mathematical, and statistical calculations.

Root Mean Square Explained

Root mean square value can be defined as a changing function based on an integral of the squares of the values that occur instantly in a cycle. In other words, it is the square of the arithmetic mean or the square of the function. It is a method of taking an average of a set of numbers.

It is calculated by adding all the numbers and dividing them by the total number of points to arrive at a mean average. One can compute the mean if there is a set of data points varying around zero with positive and n values. However, the obtained value will not reveal much information about the numbers. Thus, the magnitude needs to be calculated.

The mean of the absolute values is taken to find the magnitude of numbers. This is because finding the average magnitude through finding the square root of the mean of the squares is easier when done this way. In this method, squaring the numbers makes them positive, even if they are negative. In the end, square roots of the mean of squares have to be taken to arrive at the root values.

Root mean square is different from the average. There are various ways to describe average (e.g., mean, median, or mode). The average is employed in it when stated as the arithmetic mean.

Applications

Root mean square is frequently used in various mathematical and scientific applications. One common application is in calculating the mean square value of a waveform. This is important because it tells us how much energy is contained in it as a waveform. Its one of the most popular application is in the field of electrical engineering.

For example, it is often used to calculate the magnitude of an alternating current or voltage. It can also be used to determine the power dissipation of a resistor. Another application is in calculating the power required to drive a certain load. It can also be used to measure the variability of a data set. Finally, in physics, it is sometimes used to calculate the average kinetic energy of particles.

The root mean square error is used to measure how the magnitude of dispersion of residuals or prediction errors in a calculation. It denotes the difference between the predicted and observed results.

Formula

The root mean square value of a given set of "n" discrete observations can be given by the formula:

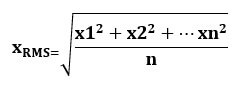
Where x = data values given

And n = total number of items

The values are squared first, and the average of all the squared values are taken. After that, the square root of the average is taken.

For a continuous set of values, its formula can be:

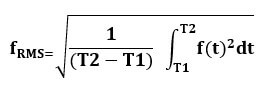
Where a continuous set of observations are taken between the time interval T1<t<T2

A root mean square calculator available online can also be used to easily calculate it.

Calculation Example

Now let us see how root mean square is calculated with the help of an example.

Let the values be 2, 4, and 6,8,10.

Step1:

The square of these values is taken.

22=4

42=8

62=36

82=64,

102=100

The new values that arrived are 4, 8, 36, and 64,100.

Step 2:

The averages of the squares shall be taken

Average=(4+8+36+64, 100)/5= 212/5= 42.4

Step 3:

The final step shall be to take the square root of the average. Therefore the root mean square value will be = 6.5115.

Frequently Asked Questions (FAQs)

How to calculate the root mean square?

True root mean square of a given set of observations can be calculated in three easy steps. First, squares for each value given shall be calculated. Then, the average of the acquired squares shall be determined. Finally, in the third step, we can compute the square root of the averages.

Why use root mean square instead of average?

RMS is utilized when the variables provided in the data set are both positive and negative. At the same time, an average as a function is used to determine the central tendency of a specific data set.

Can root mean square to be negative?

The values given are squared in order to remove any negative numbers. The root mean square will always be positive since the squared sum is positive.

What is the difference between root mean square and mean square?

The arithmetic mean of the squares of a group of numbers or a random variable is the mean square. The true RMS is the square root of a mean square and can be used to calculate its deviation.