Risk Return Trade Off

The risk return trade-off is one of the fundamental aspects that investors consider while making each investment choice and evaluating their investments. The risk-return tradeoff is a notion of trading that connects high levels of risk with high levels of gain.

The optimal risk-return trade-off is determined by several different criteria, including an investor's risk tolerance, the number of years until the person retires, and the investor's ability to replenish lost assets. This trade-off states that for an investor to reap bigger returns from the money invested, they must first be willing to tolerate a greater likelihood of incurring losses.

• The risk-return trade-off is a theory of investing that states that an asset's potential return will be proportional to the level of risk the investor takes.
• Investors examine the investment's alpha, beta, standard deviation, and Sharpe ratio to ascertain the risk-return tradeoff of a particular stock or mutual fund.
• When determining an adequate risk-return trade-off, investors must consider several aspects, including their general risk tolerance, the possibility of replacing lost cash, and several other criteria.
• Investors consider the risk-return trade-off when deciding how to allocate their capital among their many portfolios and individual assets.

According to the risk-return trade-off, the potential reward should increase if there is also an increase in risk. Individuals tend to link low levels of uncertainty with low potential rewards, whereas high levels of uncertainty or risk are associated with large potential returns. This is because of the uncertainty principle.

When selecting a portfolio with acceptable levels of risk and return, time is also an extremely important factor to consider. For instance, if an investor can invest in equities over a long period, they can recover from the risks associated with bear markets and participate in bull markets. On the other hand, if an investor can only invest for a short period, the same equities have a greater risk proposition.

At the portfolio level, the risk-return trade-off might involve assessments of the concentration or the diversification of holdings. The trade-off question is choosing between an excessive risk or a possibility for lower returns.

Let us look at the formula for calculating risk-return trade-offs in mutual funds.

#1 Alpha

A mutual fund investor's capacity to produce returns is one of the factors that is taken into account while calculating alpha. The ratio of a mutual fund scheme's risk-adjusted returns to those of its underlying benchmark is referred to as the alpha. When a scheme's alpha is negative, the fund has underperformed compared to its benchmark. When it comes to returns, a greater alpha signifies better performance.

Alpha = (Mutual Fund Return – Risk Free Return (Rf­)) – .

#2 Beta

A mutual fund portfolio's beta indicates how sensitive it is to changes in the market. The fund's response to changes in the market can be better understood with the aid of beta. In addition, the sector's beta or benchmark invariably equals one. When matched to its respective benchmark index, a fund's beta that is lower than one indicates that the fund experiences less volatility.

On the other side, if a fund's beta is greater than one, it indicates a higher volatility level than its benchmark. Investors new to the market or risk-averse should look for funds with less than one beta since these funds are less volatile. Those willing to take on more risk might select funds with a higher beta.

Beta = (Mutual Fund Return – Risk-Free Rate (Rf­)) / (Benchmark Return – Risk-Free Rate (Rf­)).

#3 Sharpe Ratio

The Sharpe ratio is a performance indicator that may be utilized to assist in predicting the prospective risk-adjusted returns of a mutual fund investment strategy. The return that a mutual fund strategy provides, in addition to the risk-free rate of return, is referred to as the risk-adjusted return for that strategy. In layperson's terms, a Sharpe ratio is a tool that assists in determining the possible returns that a strategy can generate in comparison to each unit of risk it assumes. Compared to the possibility of loss, a higher ratio indicates a greater return on investment.

Sharpe Ratio = (Mutual Fund Returns – Risk-Free Rate) / Standard Deviation.

#4 Standard Deviation

A portfolio return's standard deviation can determine how much it deviates from the average. In other words, a mutual fund's standard deviation demonstrates how far its performance deviates from predicted returns. A fund with a larger standard deviation exhibits greater volatility and entails greater risk than one with a smaller standard deviation. Standard deviation, as opposed to just market-related volatility, evaluates overall risk.

Standard Deviation = √( (∑ (x_i- x ̅ )² )/(n-1))

Here-

X_i is the i^th point in the data set
X̅ is the mean value of the data set
N is the total number of data points in the set

Analysts might utilize standard deviation when comparing two funds in the same category as a performance comparison. One must compare the standard deviation to other funds in the same category to establish whether it is high or low.

When making an investment decision, the four above mentioned indicators are utilized to determine the risk associated with certain equities and mutual funds. A greater emphasis is laid on creating a well-diversified portfolio to hedge against market volatility. Every investment also involves a risk versus return trade-off. As a result, you must concentrate on your investment goal, time horizon, and level of risk tolerance for risk-return trade-offs to fit the investment portfolio.

For instance, an individual named Sara is deciding whether or not to invest. She wants to balance the potential for loss against the potential for gain. She will get a modest return if she puts all her money into a savings account. However, it corresponds to the interest rate that the bank pays. Still, the bank will ensure her money is up to USD 5,000.

On the other hand, if she puts her money into stocks and shares, she risks losing a significant portion of her wealth. However, this has the potential to earn a far larger return on investment compared to a bank savings account. Thus this is the trade-off she will have to make, implying choosing to be open to risk for a bigger gain.

The unspoken relationship between risk and return defines the conceptual foundation for the interaction between decision-makers and the market.

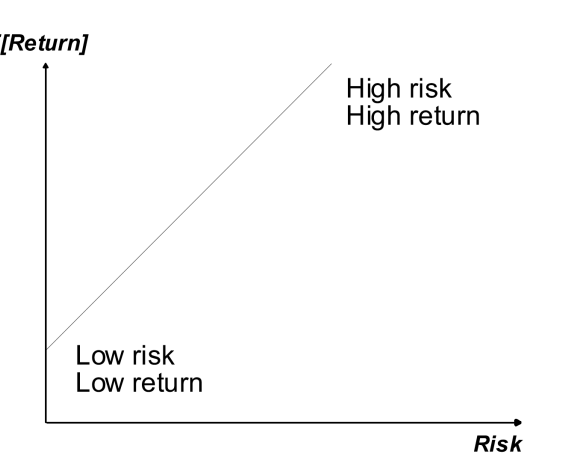
The above diagram is part of a research paper on exploiting stock data. The graph states that the decision-maker profile reflects the balance between return and risk. It is often known as risk tolerance (risk averse, risk loving). It is conveyed in the market that investments with more risk have higher projected returns. The potential that the predicted return will be a loss proportional to the risk becomes more likely as the risk level of the investment increases. Therefore, managing the risk-return trade-off is the primary focus of an investor's activity in the investing game.

The risk return trade off serves as the foundation for building portfolios. Additionally, the passage of time is an important consideration. One has a greater desire for larger returns for a longer time horizon. Thus it gives the financial flexibility to take on more risks.

It helps with financial planning by establishing a good balance between risk and return on investments. In addition, it is the most effective method for understanding the various asset classes. Also, it explains the risks that are connected with each asset class. This contributes to the success of attaining financial goals.

The risk-return trade-off is beneficial to the optimization of a portfolio. The term portfolio optimization refers to minimizing risk. It considers the level of return or maximizing profits in exchange for a given level of risk. When investors understand the amount of risk, they can segment it into various asset classes.

This has been a guide to what is Risk Return Trade-Off. We explain it in detail with its example, importance, formula, calculation, and diagram. You can learn more about finance from the following articles –

• Risk-Seeking
• Value At Risk
• Excess Return