Table Of Contents
What Is Returns to Scale?
Returns to scale in economics refers to a term that states that the degree of change in input factors changes the output proportionally and concurrently during the production process. It reflects the quantitative change that applies in the long-term using similar technology. It forms the basis of measuring a firm's or industry's efficiency of production capacity.
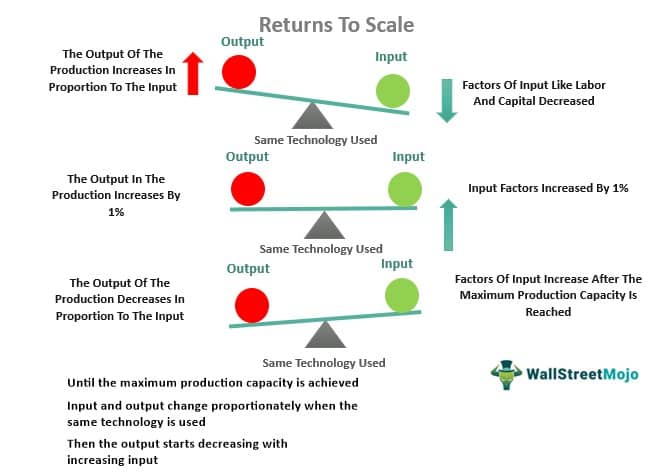
As per the law, a firm has to bear less cost of production when output increases with an increase in output factors and vice versa. Therefore, it is helpful for firms, businesses, and organizations to know their maximum production capacity. It is also important for the government to decide whether an industry will be of small or large manufacturers.
Table of contents
- Returns to scale in economics is the measure of proportional change in output with respect to the input factors in the long run at constant technology used for the production process.
- It helps measure the efficiency of a firm and policy formation in industry categorization and allows the maximum capacity of production of a firm.
- Its assumptions include - only two inputs, fixed technology, constant pricing, and labor plus capital used as inputs.
- There are three types of return to scale – constant returns to scale, increasing returns to scale, and decreasing returns to scale.
Returns To Scale Explained
Returns to scale in economics is a term that defines the relationship between the input changes in proportion with the output during production using the same type of technology. It reflects the change or variation in productivity. A producer commonly uses inputs such as labor and capital to produce goods and services. Therefore, it is the best method to measure the efficiency of production. The lesser the amount of input a producer uses to produce more output, the better its efficiency, and vice versa.
In the manufacturing sector, it is a commonplace to have the highest output level with minimum raw material inputs like labor and capital. However, all factors of production are variable in the long run. So, by changing the production factor's quantity, producers can change the production scale and make it optimal. For example, to increase the production output, firms must change the input levels proportionally and utilize them to the best capacity. During such a scenario, it is necessary to find the relationship between changes in input with the changes in output during production.
While applying the law of returns to any factory, one has to consider these assumptions:
- Producers should consider using only capital and labor as input factors of production.
- Producers should add both labor and capital together in a fixed ratio.
- The prices of these factors remain constant.
Producers use the same technology in the long term.
Returns To Scale Graph
After considering all the above assumptions, the changes in inputs at the same level led to proportional changes in the production process during the long term at the same level of technology. The input changes can lead to three types of proportional output: constant, increasing, or decreasing/diminishing returns to scale. Economists or producers can represent it in a graph.
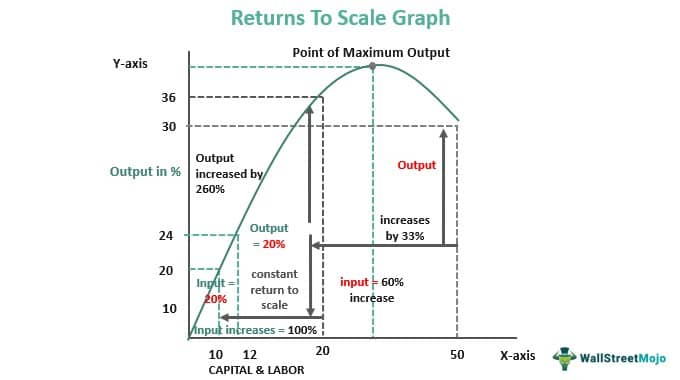
The X-axis represents the labor and capital, and the Y-axis represents the output.
One can observe from the graph that at the same level of technology and after applying the assumptions, one gets the following values.
| Nature of law of return applicable | Level of input changes (%) | level of output changes (%) |
|---|---|---|
| Increasing the law of returns | 100% | 260% |
| Constant law of returns | 20 | 20 |
| Decreasing the law of returns | 60 % | 33% |
Types
Thus, any proportional change in a firm's input can lead to variable output proportions depending on production efficiency. Here are the three types of returns to scale:
#1 - Constant Returns To Scale
It means that increasing the input in proportion to the output gives the same level of increase in the output during the production. For illustration, let a firm increase the input to three times, then the output level will also be three times during the process of production (figure 2). So, it happens during the long term of the production process for a firm.
Here, internal and external equals the internal and external diseconomies. A good example of this homogeneous production function is the Cobb-Douglas linear homogenous production function.
#2 - Increasing Returns To Scale
One can also refer to it as diminishing cost. It happens when an increase in inputs of production by a small proportion as compared to output produces an unexpected higher proportion of the output. For example, if the producers doubled the input concerning the output, the production tripled output (figure 2). Hence, one can say that the firm has experienced an increasing return to scale. It also happens during the long term of the production process for a firm, causing increasing RTS. Finally, it occurs due to the increase in efficiency of a firm's production by factors like division of labor.
#3 - Decreasing Returns to Scale
One can also refer to diminishing returns to scale as increasing cost. It means that the increase in input corresponding to the output leads to a decrease in output as expected during the production process. For instance, if a factory increased the input by 60% concerning the output during the production process, but the output was only 33%, then the firm is said to go through decreasing scale returns (figure 2).
The decreased efficiency or production of a firm causes it.
Example
Here is a return to scale example to understand the concept better.
For this purpose, let's assume the Apple iPhone store has ten kiosks for servicing the customers who come to service their iPhones. In this way, they can serve a total of 100 customers every week. But they were facing 150 customers daily for servicing their iPhone. So here, one can regard the kiosk as the input and the serviceable iPhone as output.
Therefore, to serve all the customers, the store-bought five more kiosks to do the needful. As a result, the input increased by 50%, and they could serve 140 customers weekly. Hence, the store experienced an increasing return to scale. However, if they had added ten more kiosks or serviced 100% more input and only 75 customers, the weekly service may have decreased by 25%. Thus, the store might have faced diminishing returns.
Returns To Scale Formula
Let us assume that a firm's output is Y; its capital is C and labor is L, which are the inputs for the firm. Hence, one can calculate the output of the firm will be calculated as:
Y = C + L
As per the returns to scale, (R) if the inputs- a factor of m (multiplier) increases C & L, then the effect on the output Y would be as follows:
Ynew= mC + mL
Therefore, R, is new output minus old output,
i.e., Ynew – Y = (mC + mL) – (C + L)
Or, R= Ynew – Y = (mC + mL) – (C + L)
returns to scale, R= m(C-1) + m(L-1)
Frequently Asked Questions (FAQs)
The causes of increasing returns to scale are:
Division of labor and increased efficiency of variable factors.
Maximum utilization of the fixed factors
Organized and efficient coordination between the factors.
Internal and external economies
Indivisibility of factors of production.
One can calculate it using the below formula:
returns of scale, R= m(C-1) + m(L-1) where C = capital, L = labor
The assumptions of the law of returns to scale are:
Using fixed technology
Uses only capital & labor in a fixed ratio
Factors affecting price are constant
Diminishing returns means that once the production level has reached its maximum point, increasing any of the two inputs during production negatively impacts the output. In other words, after the output reaches a maximum point, it decreases and eventually becomes negative with increasing the two inputs.
Recommended Articles
This has been a guide to what is Returns to Scale and its definition. Here we discuss types, formula and example of returns to scale along with its graph and detail explanation. You can learn more about accounting from the following articles –
