Regression Analysis Formula

Formula of Regression Analysis (Table of Contents)

• Formula
• Examples

What is Regression Analysis Formula?

Regression is a statistical tool to predict the dependent variable with the help of one or more than one independent variables. While running a regression analysis, the main purpose of the researcher is to find out the relationship between the dependent variable and the independent variable. In order to predict the dependent variable one or multiple independent variables are chosen which can help in predicting the dependent variable. Regression analysis helps in the process of validating whether the predictor variables are good enough to help in predicting the dependent variable.

Regression Analysis Formula

A regression formula tries to find the best fit line for the dependent variable with the help of the independent variables. The  regression analysis equation is the same as the equation for a line which is

Where,

• Y= the dependent variable of the regression equation
• M= slope of the regression equation
• x=dependent variable of the regression equation
• B= constant of the equation

Explanation

While running a regression analysis, the main purpose of the researcher is to find out the relationship between the dependent variable and the independent variable. In order to predict the dependent variable one or multiple independent variables are chosen which can help in predicting the dependent variable. Regression analysis helps in the process of validating whether the predictor variables are good enough to help in predicting the dependent variable.

Examples of Regression Analysis Formula (with Excel Template)

Let’s see some simple to advanced examples of Regression Analysis formula to understand it better.

Example #1

Let us try and understand the concept of regression analysis with the help of an example. Let us try to find out what is the relation between the distance covered by the truck driver and the age of the truck driver. Someone actually does regression equation to validate whether what he thinks of the relationship between two variables, is also validated by the regression equation. 

Below is given data for calculation of regression analysis

For the calculation of Regression Analysis go to the data tab in excel and then select data analysis option. For further procedure of calculation refer to the given article here – Analysis ToolPak in Excel

The regression analysis formula for the above example will be

• y = mx + b
• y= 575.754*-3.121+0
• y= -1797

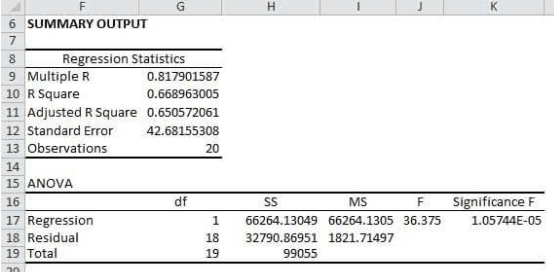
In this particular example, we will see which variable is the dependent variable and which variable is the independent variable. The dependent variable in this regression equation is the distance covered by the truck driver and the independent variable is the age of the truck driver. The regression analysis for this set of dependent and independent variable proves that the independent variable is a good predictor of the dependent variable with a reasonably high coefficient of determination. The analyzing helps in validating that the factors in the form of the independent variable are selected correctly. The snapshot below depicts the regression output for the variables. The data set and the variables are presented in the excel sheet attached.

Example #2

Let us try and understand regression analysis with the help of another example. Let us try to find out what is the relation between the height of the students of a class and the GPA grade of those students. Someone actually does regression equation to validate whether what he thinks of the relationship between two variables, is also validated by the regression equation.

In this example, Below is given data for calculation of regression analysis in excel

Regression analysis calculation, go to the data tab in excel and then select data analysis option. For the further procedure of calculation refer to the given article here – Analysis ToolPak in Excel

The regression analysis formula for the above example will be

• y = mx + b
• y= 2.65*.0034+0
• y= 0.009198

In this particular example, we will see which variable is the dependent variable and which variable is the independent variable. The dependent variable in this regression equation is the GPA of the students and the independent variable is the height of the students. The regression analysis for this set of dependent and independent variable proves that the independent variable is not a good predictor of the dependent variable as the value for the coefficient of determination is negligible. In this case, we need to find out another predictor variable in order to predict the dependent variable for the regression analysis. The snapshot below depicts the regression output for the variables. The data set and the variables are presented in the excel sheet attached.

Relevance and Uses of Regression Analysis Formula

Regression is a very useful statistical method. For any business decision in order to validate a hypothesis that a particular action will lead to the increase in the profitability of a division can be validated based on the result of the regression between the dependant and independent variables. Regression analysis equation plays a very important role in the world of finance. A lot of forecasting is done using regression analysis. For example, the sales of a particular segment can be predicted in advance with the help of macroeconomic indicators that has a very good correlation with that segment. Both linear and multiple regressions are useful for practitioners in order to make predictions of the dependent variables and also validate the independent variables as a predictor of the dependent variables.

You can download this Regression Analysis Formula Excel Template from here – Regression Analysis Formula Excel Template

Recommended Articles

This has been a guide to Regression Analysis Formula. Here we discuss how to perform Regression Analysis calculation using data analysis along with examples and downloadable excel template. You can learn more about statistical modeling from the following articles –

• What is the Coefficient of Determination?
• Definition of Gini Coefficient
• What is Adjusted R Squared?
• Regression vs ANOVA – Compare
• Regression Analysis Excel
• Formula of R Squared
• Formula of Forecast in Excel