R-squared (R2) is an important statistical measure. A regression model represents the proportion of the difference or variance in statistical terms for a dependent variable that an independent variable or variables can explain. In short, it determines how well the data will fit the regression model.

• R-squared (R2) is an essential statistical tool. A regression model shows the difference or variance proportion in statistical terms for a dependent variable that an independent variable or variables can explain. Then, it calculates the data that fits the regression model.
• For the R-squared calculation, one must estimate the correlation coefficient and then square the result.
• The R-squared relevance in regression is the capability to search the probability of the future event happening in the forecasted results or the outcomes. 

Suppose there is any relationship or correlation which may be linear or non-linear between those two variables. In that case, if there is a change in the independent variable in value, the other dependent variable will likely change in value, say linearly or nonlinearly.

The numerator part of the formula tests whether they move together and remove their movements. The relative strength of both of them moving together. The denominator part of the formula scales the numerator taking the square root of the product of the differences between the variables from their squared variables. And when you square this result, we get R-squared, which is nothing but the coefficient of determination.

Example #1

Consider the following two variables x and y, you are required to calculate the R Squared in Regression.

Solution:

Using the formula mentioned above, we need to first calculate the correlation coefficient.

We have all the values in the above table with n = 4.

Let’s now input the formulas' values to arrive at the figure.

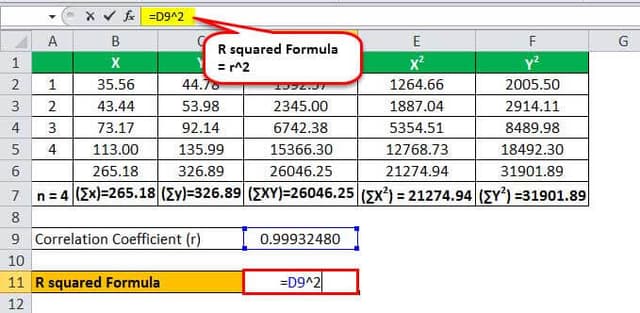
r = ( 4 * 26,046.25 ) – ( 265.18 * 326.89 )/ √ *

r = 17,501.06 / 17,512.88

The Correlation Coefficient will be-

r = 0.99932480

So, the calculation will be as follows,

r² = (0.99932480)²

R Squared Formula in Regression

r² = 0.998650052

Example #2

India, a developing country, wants to conduct an independent analysis of whether changes in crude oil prices have affected its rupee value. Following is the history of Brent crude oil price and rupee valuation, both against dollars that prevailed on an average for those years below.

Solution:

Using the formula for the correlation above, we can calculate the correlation coefficient first. Treating average crude oil price as one variable, say x, and treating Rupee per dollar as another variable as y.

RBI, the Central Bank of India, has approached you to provide a presentation on the same in the next meeting. But, first, determine whether the movements in crude oil affect movements in the rupee per dollar.

Solution:

Using the formula for the correlation above, we can calculate the correlation coefficient first. For example, treating average crude oil price as one variable, say x, and treating rupee per dollar as another as y.

We have all the values in the above table with n = 6.

Let’s now input the formulas' values to arrive at the figure.

The Correlation Coefficient will be-

r = (6 * 23592.83) – (356.70 * 398.59) / √ *

r = -620.06 / 1,715.95

r = -0.3614

So, the calculation will be as follows,

r² = (-0.3614)²

R Squared Formula in Regression

r² = 0.1306

Analysis: There is a minor relationship between changes in crude oil prices and the price of the Indian rupee. As crude oil price increases, the changes in the Indian rupee also affect. But since R-squared is only 13%, the changes in crude oil price explain very little about changes in the Indian rupee. The Indian rupee is also subject to changes in other variables, which must account for.

Example #3

XYZ laboratory is researching height and weight and is interested in knowing if there is any relationship between these variables. After gathering a sample of 5000 people for every category and came up with an average weight and height in that particular group.

Below are the details that they have gathered.

You are required to calculate R-squared and conclude if this model explains the variances in height affect variances in weight.

Solution:

Using the formula for the correlation above, we can calculate the correlation coefficient first. For example, treating height as one variable, say x, and weight as another as y.

We have all the values in the above table with n = 6.

Let’s now input the values in the formula to arrive at the figure.

r = ( 7 * 74,058.67 ) – (1031 * 496.44) / √ *

r = 6,581.05 / 7,075.77

The Correlation Coefficient will be-

Correlation Coefficient (r) = 0.9301

So, the calculation will be as follows,

r² = 0.8651

Analysis: The correlation is positive. It appears there is some relationship between height and weight. As the height increases, the person's weight also appears to increase. While R2 suggests that 86% of changes in height attributes to changes in weight, 14% are unexplained.

The relevance of R-squared in regression is its ability to find the probability of future events occurring within the given predicted results or the outcomes. If more samples are added to the model, the coefficient will show the likelihood or the probability of a new point or the new dataset falling on the line. The determination does not prove causality even if both variables have a strong connection.

Some of the spaces where R squared is mostly used is for tracking mutual fund performance, tracking risk in hedge funds, and determining how well stock moves with the market, where R2 would suggest how much of the stock can be explained by the movements in the market.

This article has been a guide to R-Squared Formula in Regression. Here, we learn how to calculate R-Square using its formula, examples, and a downloadable Excel template. You can learn more about financial analysis from the following articles: -

• Adjusted R Squared
• Correlation Formula
• Formula of Regression 
• Examples of Linear Regression