R-Squared

R-squared ( R² or Coefficient of Determination) is a statistical measure that indicates the extent of variation in a dependent variable due to an independent variable. In investing, it acts as a helpful tool for technical analysis. It assesses the performance of a security or fund (dependent variable) with respect to a given benchmark index (independent variable).

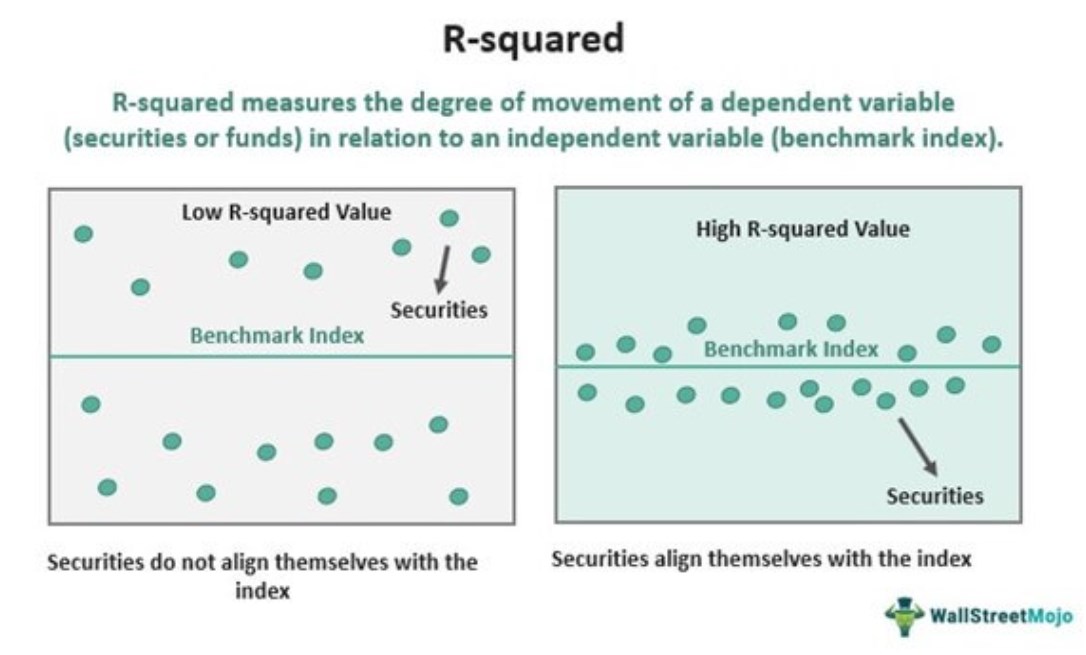
Unlike correlation (R) which measures the strength of the association between two variables, R-squared indicates the variation in data explained by the relationship between an independent variable and a dependent variable. R2 value ranges from 0 to 1 and is expressed in percentage. In finance, it indicates the percentage to which securities move in response to the movement of the index. The higher the value of R-squared, the more in sync the movement of securities with the index and vice-versa. As a result, it helps investors to keep track of their investments.

• R-squared measures the degree of movement of a dependent variable (stock or funds) in relation to an independent variable (benchmark index).
• It helps in knowing a security's performance against the benchmark index.
• The higher the value of R², the more dependent the dependent variable's performance on the independent variable and vice versa.
• The values of R² are represented as a percentage ranging from 1 to 100 percent.
• R, R², and adjusted R² are different terminologies in statistics. R presents the correlation between variables, R² indicates the variation in data explained by the correlation, and adjusted R² takes other variables into account.

To arrive at R², do the following:

1. Determine the correlation coefficient (R)

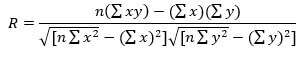
where,

• n = Number of observations
• Σx = Total value of the independent variable
• Σy = Total value of the dependent variable
• Σxy = Sum of the product of independent and dependent variable
• Σx² = Sum of the squares of the independent variable value
• Σy² = Sum of the squares of the dependent variable value

2. Square the correlation coefficient (R)

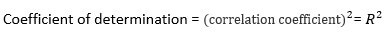
The value of R² lies within the range of 0 and 1. It means if the value is 0, the independent variable does not explain the changes in the dependent variable. However, a value of 1 reveals that the independent variable explains the variation in the dependent variable perfectly well. Typically, R² is expressed in the form of a percentage for easy reference.

Here are some examples to get clarity on the concept of R-squared.

Example #1

Let us find out the relation between the number of articles written by journalists in a month and their number of years of experience. Here, the dependent variable (y) is the number of articles written and the independent variable (x) is the number of years of experience.

First, find the correlation coefficient (R) and then square it to get the coefficient of determination or R². Here is the data.

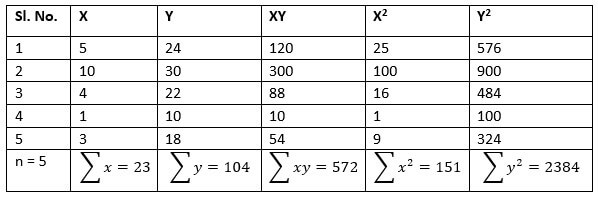
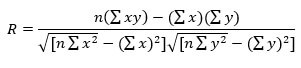
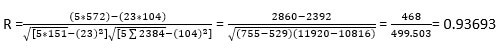
R²= 0.93²= 0.8649

Therefore, the coefficient of determination is 86%. It means 86% of variations in the number of articles written are explained by the writer's years of experience.

Example #2

Suppose an investor wants to monitor his portfolio by looking at S&P Index. Therefore, he wishes to know the correlation between his portfolio returns and the benchmark index. So, he calculates R and R-squared. A high R-squared value indicates a portfolio that moves like the index.

Here is a list of portfolio returns represented by the dependent variable (y) and the benchmark index’s returns indicated by the independent variable (x).

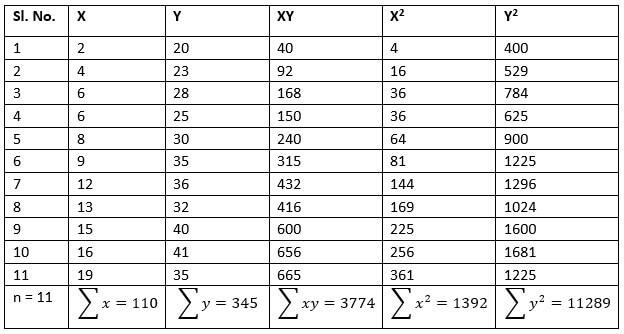
Finally, R2 is calculated using the formula:

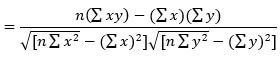
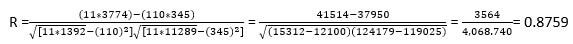
R² = ²  

     = 0.7672

The value of R2 implies that 76.72% variation of portfolio returns is in accordance with the S&P Index. Thus, the investor can track the movements of his portfolio by monitoring the index.

R-squared measures the effect of variation in the independent variable on the movement of the dependent variable. In stock markets, it is the percentage by which the securities move in response to the movement of a benchmark index like the S&P Index.

If one wants a security portfolio that is in sync with the benchmark index, it should have a high R² value. However, if one wishes that the benchmark does not impact the security portfolio performance, then one has to look for a portfolio which is having low R² value.

In other words, if the value of R² is in the range of:

• 70-100 % then the security portfolio has the highest relationship with the movement and return of the benchmark indices
• 40-70%, then the relationship between the returns of portfolio and the returns of benchmark indices is average
• 1-40%, then there is very little or no connection between the returns of the portfolio and the returns of the benchmark index

Both R² and adjusted R² are used to measure the correlation between a dependent variable and an independent variable. On the one hand, R² represents the percentage of the variance in a dependent variable described by an independent variable. While on the other hand, adjusted R² is a revised version of R-squared that is adjusted for the number of independent variables used.  

Adjusted R-squared provides a more accurate correlation between the variables by considering the effect of all independent variables on the regression function. As a result, it is easy to identify the exact variables affecting the correlation. In addition, it helps to know which variables are more important than the other.

R-squared tends to increase upon adding independent variables to the data set. However, an adjusted R² can remove this flaw. Therefore, whenever the added variables are insignificant or negative, then the adjusted R² value decreases or adjusts accordingly. Hence, one can say that adjusted R² is more reliable than R².

R or correlation coefficient is a term that conveys the direct relationship between any two variables like returns and the risk of a security. The range of R is between -1 to 1. The negative value denotes an inverse relationship, and +1 indicates the direct relationship between the variables.

R² is used in data set that contains multiple variables of different properties like risk, return, rate of interest, and length of maturity in security. The range of R² is between 0 to 1, with 0 being a poor indicator and 1 being an excellent one.

This article has been a Guide to R-Squared & its Meaning. Here we discuss R-Squared its formula, value interpretation in regression, examples, & difference with R. You can learn more about economics from the following articles –

• Econometrics
• Multiple Regression Formula
• Nonlinear Regression