Table Of Contents
What is Present Value of Annuity?
The present value of annuity is the present value of future cash flows adjusted to the time value of money considering all the relevant factors like discounting rate (specific rate). Finding out the present value of future cash flows helps investors to understand how much money they will receive over a period of time in today’s dollar’s terms and make informed investment decisions.
Because of inflation, the purchasing power of money gets diminished, so because of the time value of money concept, money received today has more value than money, which will be received tomorrow. In simple terms, we can say that if one has money now, they can invest that money and enjoy returns on that money, so automatically, the value of money gets appreciated.
Table of contents
- The concept of the present value of annuity emphasizes that money today is worth more than the same amount in the future.
- The present value of an annuity involves discounting future cash flows to determine their current value.
- A lower discount rate increases the present value of an annuity, as it assumes a lower opportunity cost and lower risk associated with investing that money elsewhere. Conversely, a higher discount rate decreases the present value of an annuity.
Present Value Of Annuity Explained
The present value of annuity is the present value of payments in the future from the annuity at a particular rate of return or a discount rate. It is important to note that the current value is inversely proportional to the discount rate. As in, the higher the discount rate, the lower the current value of the investment.
It is a well-established fact that inflation reduces the value of money over time and the money in today’s terms is more valuable than the same amount in the future. By the same logic, the $ 10,000 money received today is more worthy than the $ 10,000 received tomorrow.
The present value of annuity table is one of the very important concepts to figure out the actual value of future cash flows. The same formula can be used for cash inflows as well as cash outflows. For cash inflows, one can use the term discount rate whereas, for cash outflows, the term interest rate can be used.
By using the same concept, an investor can find out the present value of future cash flows, either incoming or outgoing. The normal formula can help us find the present value of an annuity if cash flows are at the end of the period. But if cash flows are at the period’s beginning, then the annuity due formula will help.
Formula
Before we get to using the present value of annuity calculator, it is important to understand its formula to calculate the same. It is the very basis of the concept and its related factors.
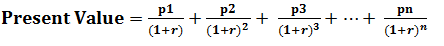
Here,
- p1, p2 – Annuity payments,
- r – Discount rate
- n – Time Period in years
After simplifying this Present value of annuity formula, we can get
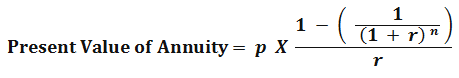
Here,
- p – Equated annual payments
- r – Discount rate
- n – a time period in years
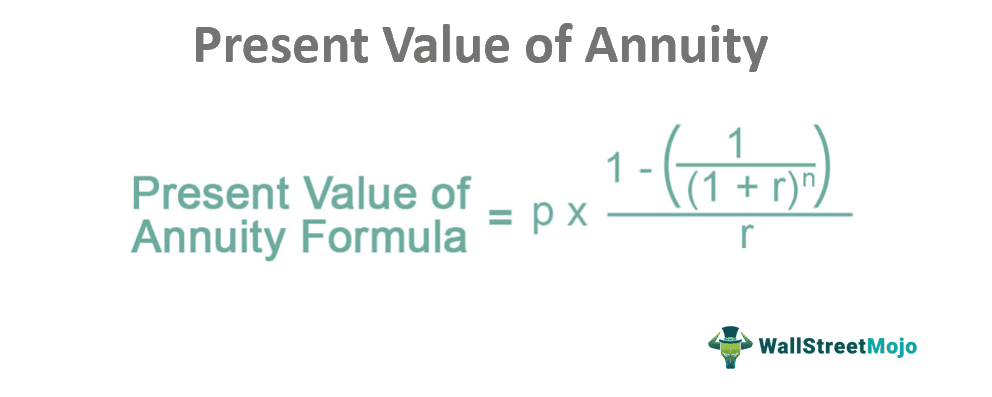
How To Calculate?
The present value of annuity calculator shows how much the annuity and determines the fairness of the deal when the payments are sold. However, to be able to calculate this using the formula, the following data must be gathered beforehand:
- Amount of each fixed payment, in Dollars
- Number of payments intended to be sold
- Discount rate, if any
Examples
Let us understand the concept of present value of annuity table and other related factors with the help of a couple of examples. These examples will help us understand the intricacies of the concept.
Example #1
Mr. ABC is a 60 years old, retired Government servant. He has been paying into his retirement account per month for the last 30 years, and now, after his retirement, he can start withdrawing funds from the retirement account. As per the agreement, the retirement company is giving him to pay $ 30,000 on the 1st of each year for the next 25 years, or another option is a one-time payment of $ 500,000. Now Mr. ABC wants to know what is the value of the $30,000 yearly payments made to him compared to a one-time payment. He has the option to choose, and he wants to choose, which gives him more money.
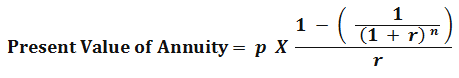
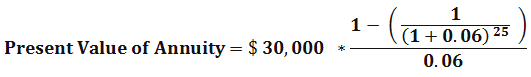
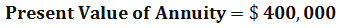
By using the above present value of annuity formula calculation, we can see now, annuity payments are worth about $ 400,000 today, assuming the interest rate or the discount rate at 6 %. So Mr. ABC should take off $ 500,000 today and invest by himself to get better returns.
Using the present value formula above, we can see that the annuity payments are worth about $400,000 today, assuming an average interest rate of 6 percent. Thus, Mr. Johnson is better off taking the lump sum amount today and investing in himself.
Here, if we change the discount rate, then the present value changes drastically. The discount factor can be taken based on the interest rates or cost of funds for the company. It depends upon the usage of the discount factor. Thus, the lower the discount rate, the higher the present value.
Example #2
Find out the annuity of $ 500 paid at the end of each month of the calendar years for one year. The annual interest rate is 12 %.
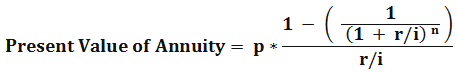
Here,
i – Frequency of occurrences
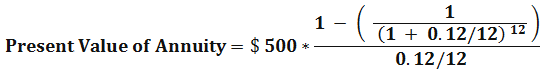
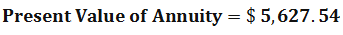
Present value Annuity Factor
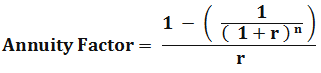
Here,
- r – Discount rate
- n – the time period in years
For the sake of simplicity and ease of using financial models, professionals usually calculate present value annuity factors, which helps them to keep an eye on discount rates as well as total annuity factors.
This factor is maintained into tabular forms to find out the present value per dollar of cash flow based on the periods and the discount rate period. Once the value of dollar cash flows is known, the actual period cash flows are multiplied by the annuity factor to find out the present value of the annuity.
Annuity Due
Until now, we have seen the present value of annuity table payments done at each period’s end. What if payment is made at the start of the period, then the above formula could be misleading. The annuity can help us in finding out the present value of an annuity whose payment is made at the starting date of the period.
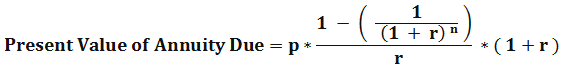
Here,
- p – Equated annual payments
- r – Discount rate
- n – the time period in years
Frequently Asked Questions (FAQs)
The discount rate is a crucial factor in determining the present value of an annuity. It represents the rate of return or the cost of capital used to discount future cash flows. Therefore, a higher discount rate will result in a lower present value, as future cash flows are considered less valuable when discounted at a higher rate.
No, the present value of an annuity cannot be negative. Hence, this is because the concept of present value involves determining the value of future cash flows in today's terms, and a negative present value would imply that the annuity has a negative worth. However, the present value can be zero, indicating that the annuity's cash flows are precisely equivalent to the initial investment or have no value in today's terms.
The time, represented by the number of periods (n), significantly impacts the present value of an annuity. As the number of periods increases, the present value of the annuity decreases. Hence, this is because the longer it takes to receive future cash flows, the more they are discounted to reflect the time value of money.
Recommended Articles
This has been a guide to what is Present Value of an Annuity. Here we explain its formulas, how to calculate, annuity due, and examples in detail. You can learn more from the following articles –
