Present Value Formula

Last Updated :

-

Blog Author :

WallStreetMojo Team

Edited by :

Ashish Kumar Srivastav

Reviewed by :

Dheeraj Vaidya, CFA, FRM

Table Of Contents

arrow

Formula to Calculate Present Value (PV)

Present value, a concept based on time value of money, states that a sum of money today is worth much more than the same sum of money in the future and is calculated by dividing the future cash flow by one plus the discount rate raised to the number of periods.

Table of contents
  • The present value formula recognizes the principle of the time value of money.
  • Time plays a crucial role in the present value formula. The longer the period, the greater the discounting effect on future cash flows. Therefore, future cash flows further into the future have a lower present value compared to those occurring sooner.
  • The interest rate used in the present value formula represents the required rate of return or discount rate.
  • The present value formula provides a helpful tool for making financial decisions. By calculating the current value of future cash flows, individuals and businesses can compare different investment options and assess the profitability of projects.
PV = C / (1 + r) n
Present-Value-Formula

where, PV = Present value

  • C = Future cash flow
  • r = Discount rate
  • n = Number of periods

For a series of future cash flows with multiple timelines, the PV formula can be expressed as,

PV = C1 / (1 + r) n1 + C2 / (1 + r) n2 + C3 / (1 + r) n3 + ……. + Ck / (1 + r) nk

Calculation of Present Value (Step by Step)

The calculation of the PV Formula can be done by using the following steps:

  1. Firstly, determine the future cash flows for each period, which are then denoted by Ci where i varies from 1 to k.

  2. Next, determine the discount rate or the specified rate at which the future cash flows have to be discounted. It is a very important factor and is decided either on the basis of the market trend or the risk appetite of the investor. The discount rate is denoted by r.

  3. Next, determine the number of periods for each of the cash flows. It is denoted by n.

  4. Next, calculate the present value for each cash flow by dividing the future cash flow (step 1) by one plus the discount rate (step 2) raised to the number of periods (step 3).

  • PVi = Ci / (1 + r) ni
  • PV = C1 / (1 + r) n1 + C2 / (1 + r) n2 + C3 / (1 + r) n3 + ……. + Ck / (1 + r) nk

Examples

Example #1

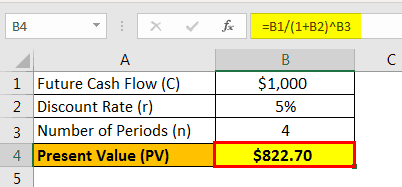
Let us take the example of John who is expected to receive $1,000 after 4 years. Determine the present value of the sum today if the discount rate is 5%.

Given,

  • Future cash flow, C = $1,000
  • Discount rate, r = 5%
  • Number of periods, n = 4 years

Therefore, the present value of the sum can be calculated as,

Present Value Example 1.1png

PV = C / (1 + r) n

= $1,000 / (1 + 5%) 4

Present Value Example 1.2png

PV = $822.70 ~ $823

Example #2

Let us take another example of a project having a life of 5 years with the following cash flow. Determine the present value of all the cash flows if the relevant discount rate is 6%.

  • Cash flow for year 1: $400
  • Cash flow for year 2: $500
  • Cash flow for year 3 : $300
  • Cash flow for year 4: $600
  • Cash flow for year 5: $200

Given, Discount rate, r = 6%

Cash flow, C1 = $400              No. of period, n1 = 1

Cash flow, C2 = $500              No. of period, n2 = 2

Cash flow, C3 = $300              No. of period, n3 = 3

Cash flow, C4 = $600              No. of period, n4 = 4

Cash flow, C5 = $200              No. of period, n5 = 5

Present Value Example 2

Therefore, calculation of present value of cash flow of year 1 can be done as,

PV Example 2.1png

PV of cash flow of year 1, PV1 = C1 / (1 + r) n1

= $400 / (1 + 6%)1

PV of cash flow of year 1 will be -

Present Value Example 2.2png

PV of cash flow of year 1 = $377.36

Similarly, we can calculate PV of cash flow of year 2 to 5

  • PV of cash flow of year 2, PV2 = C2 / (1 + r) n2

= $500 / (1 + 6%)2

= $445.00

  • PV of cash flow of year 3, PV3 = C3 / (1 + r) n3

= $300 / (1 + 6%)3

= $251.89

  • PV of cash flow of year 4, PV4 = C4 / (1 + r) n4

= $600 / (1 + 6%)4

= $475.26

  • PV of cash flow of year 5, PV5 = C5 / (1 + r) n5

= $200 / (1 + 6%)5

= $149.45

PV Example 2.3png

Therefore, the calculation of present value of the project cash flows is as follows,

pv Example 2.4png

PV = $377.36 + $445.00 + $251.89 + $475.26 + $149.45

PV = $1,698.95 ~ $1,699

Relevance and Uses

The entire concept of the time value of money revolves around the same theory. Another exciting aspect is the fact that the present value and the discount rate are reciprocal to each other, such that an increase in discount rate results in the lower present value of the future cash flows. Therefore, it is important to determine the discount rate appropriately as it is the key to a correct valuation of the future cash flows.

Frequently Asked Questions (FAQs)

Why is the present value formula essential?

The present value formula is essential because it allows individuals and businesses to evaluate the worth or value of future cash flows or investments in today's terms. It helps in decision-making by considering the time value of money and determining whether an investment is financially viable.

Can the present value formula be used for any cash flow?

The present value formula can be used for various cash flows, including investment returns, loan payments, annuities, and other financial transactions. It helps assess the current cash flow value that occurs at different times.

What is the net present value formula?

The net present value (NPV) formula is used to evaluate the profitability of an investment by considering the time value of money. It calculates the current value of future cash flows associated with the acquisition and subtracts the initial investment cost.