POWER Function in Excel

A POWER in Excel is a Math/Trigonometric function that computes and returns the result of a number raised to a power. The POWER Excel function takes two arguments: the base (any real number) and the exponent (power that signifies how many times the given number will be multiplied by itself). For example, 5 multiplied by a power of 2 is the same as 5 x5.

The POWER function in Excel takes both arguments as a numeric value. Hence, the arguments passed are of integer type where the number is the base number, and the POWER is the exponent. Both arguments are required and are not optional.

We can use the POWER function in Excel in many ways, like for mathematical operations. For example, we can use the POWER function equation to compute the relational algebraic functions.

The Excel POWER function is very simple and easy to use. Let us understand the working of POWER in Excel by some examples.

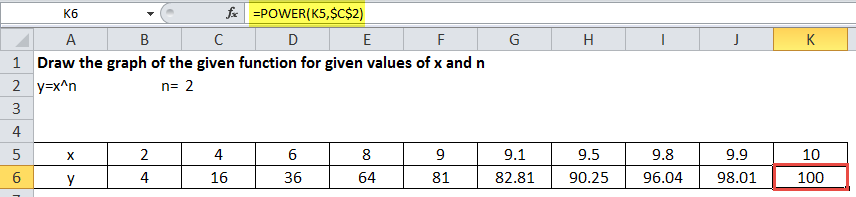
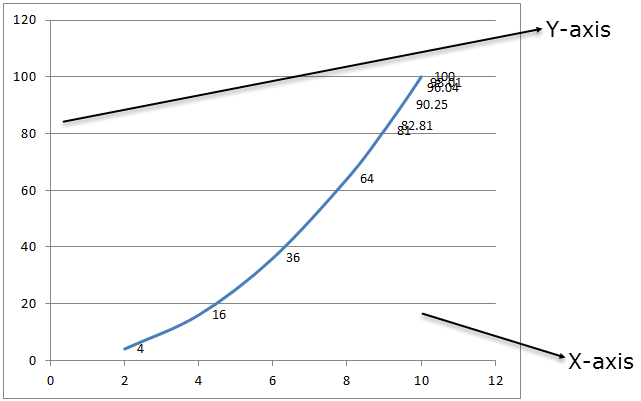
We have a POWER function equation y=x^n (x to the power n), where y is dependent on the value of x, and n is the exponent. We also want to draw the graph of this f(x, y) function for given values of x and n=2. For example, the values of x are:

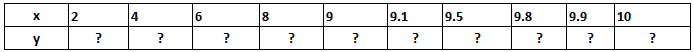
So, in this case, since the value of y depends upon the nth power of x, we will calculate the value of Y using the POWER function in Excel.

• 1^st value of y will be 2^2 (=POWER(2,2)
• 2^nd value of y will be 4^2 (=POWER(4,2)
• ……………………………………………………………
• ……………………………………………………………
• 10^th value of y will be 10^2 (=POWER(10,2)

Now, selecting the values of x and y from range B4:K5, choose the graph (in this example, we have chosen the scatter graph with smooth lines) from the "Insert" tab.

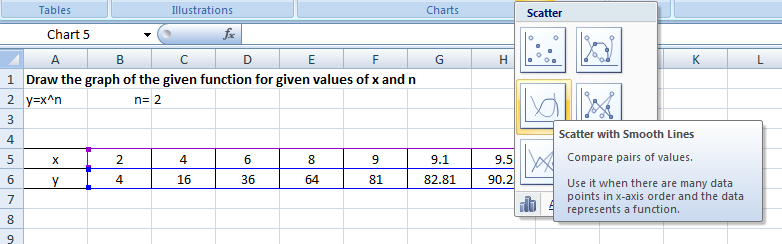
So, we get a linear, exponential graph for the given POWER function equation.

In algebra, we have the quadratic POWER function equation, represented as ax2+bx+c=0, where x is unknown, and a, b and c are the coefficients. The solution of this POWER function equation gives the roots of the equation, which are the values of x.

The roots of the quadratic POWER function equation are computed by following mathematical formula:

• x = (-b+ (b²-4ac)^1/2)/2a
• x = (-b- (b²-4ac)^1/2)/2a

b2-4ac is called discriminant and describes a quadratic POWER function equation's number of roots.

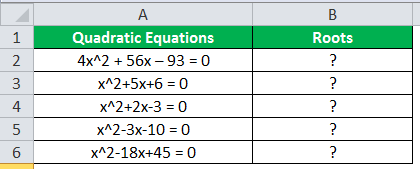
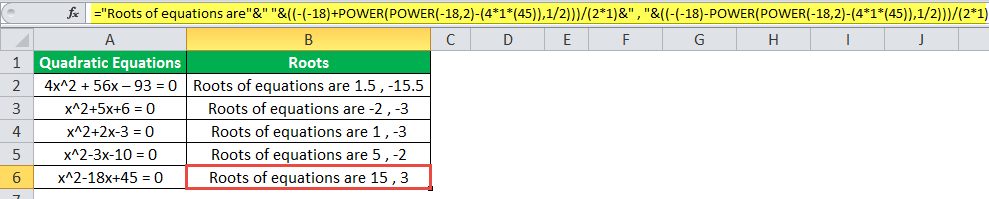
Now, we have a list of quadratic POWER function equations given in column A. But, first, we need to find the roots of the equations.

^ is the exponential operator used to represent the power (exponent). For example, X2 is the same as x^2.

We have five quadratic POWER function equations, and we will solve them using the formula with the help of the POWER function in Excel to find the roots.

In the first POWER function equation, a=4, b=56, and c = -96. If we mathematically solve them using the above formula, we have the roots -15.5 and 1.5.

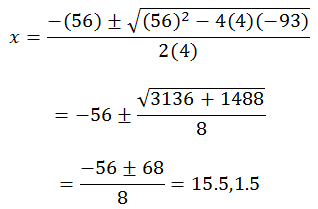
To implement this in Excel formula, we will use the POWER function in Excel and the formula will be:

• =((-56+POWER(POWER(56,2)-(4*4*(-93)),1/2)))/(2*4) will give the first root and
• =((-56-POWER(POWER(56,2)-(4*4*(-93)),1/2)))/(2*4) will give the second root of the equation

So, the complete formula will be,

="Roots of equations are"&" "&((-56+POWER(POWER(56,2)-(4*4*(-93)),1/2)))/(2*4)&" , "&((-56-POWER(POWER(56,2)-(4*4*(-93)),1/2)))/(2*4)

The formulas are concatenated with the string “Roots of equation are.”

Using the same formula for other POWER function equations, we have:

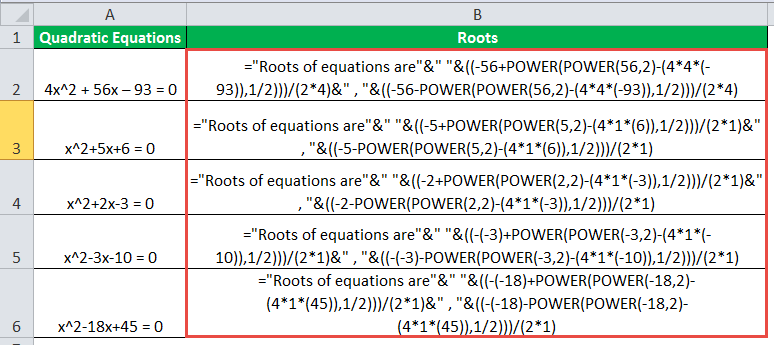
Output:

So, we can use the POWER function in Excel for different mathematical calculations.

Suppose we have to find out the compound interest for which the formula is:

Amount = Principal (1 + r/n)^nt

• Where r is the interest rate, n is the number of times interest is compounded per year, and t is the time.
• If an amount of $4,000 is deposited into an account (saving) at an interest rate of 5% annually, compounded monthly, the value of the investment after 5 years can be calculated using the above compound interest formula.
• When, Principal = $4000, rate = 5/100 that is 0.05, n =12 (compounded monthly), time =5 years.

We have the formula using the compound interest formula and implementing it into the Excel formula using the POWER function.

=B2*(POWER((1+(B3/B5)),(B4*B5)))

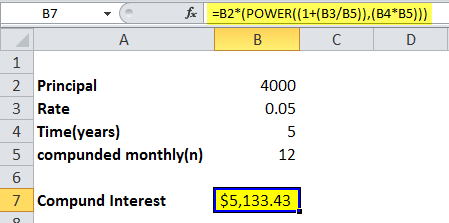
So, the investment balance after 5 years is $5.133.43.

According to Newton’s gravitation law, two bodies at a distance of r from their center of gravity attract each other in the universe according to a gravitational POWER Excel formula.

F = (G*M*m)/r²

When F is the magnitude of the gravitational force, G is called the gravitational constant, M is the mass of the first body, m is the mass of the second body, and r is the distance between the bodies from their center of gravity.

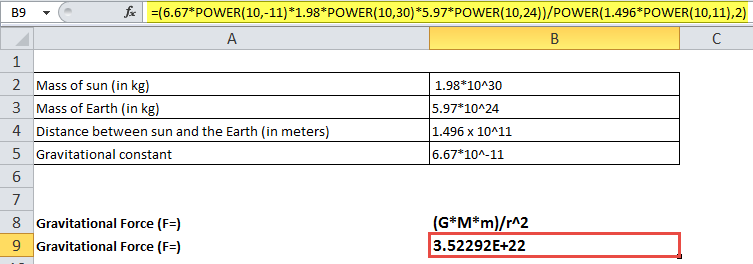
Let us calculate the magnitude of gravitational force by which the sun pulls the earth.

• The mass of the sun is 1.98*10^30 kg.
• The mass of the earth is 5.97*10^24 kg.
• The distance between the sun and the earth is 1.496 x 10^11 meters.
• Gravitational constant value is 6.67*10^-11 m3kg-1s-2.

In Excel, if we want to calculate the gravitational force, we will again be using the POWER in Excel that can operate over big numeric values.

• So, we can convert the scientific notation values into the POWER Excel formula using the POWER in Excel.
• 1.98*10^30 will be represented as 1.98*Power(10,30), similarly to other values.
• So, the POWER Excel formula to calculate the force will be: = (6.67*POWER(10,-11)*1.98*POWER(10,30)*5.97*POWER(10,24))/POWER(1.496*POWER(10,11),2)

Since the value obtained as force is a big number Excel expressed it scientific notation. To change it into a fraction, change the format to the fraction.

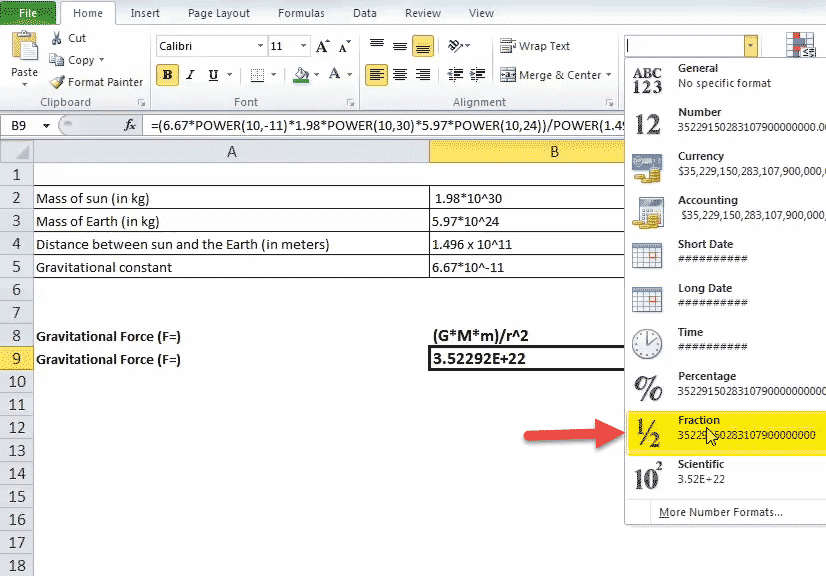
Output:

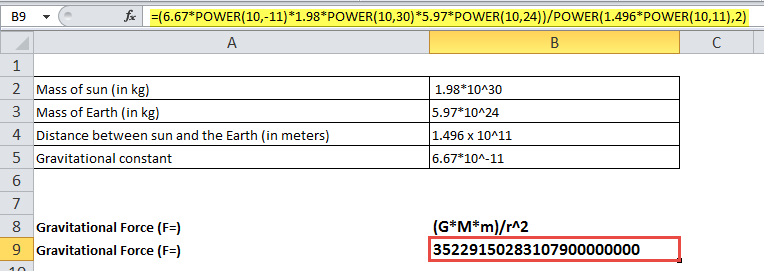
So, the sun pulls the earth with a force of magnitude 35229150283107900000000 Newton.