Point Estimators

Point Estimator Definition

A point estimator is primarily used in statistics where a sample set of data is considered, and a single best-judged value is chosen, which serves as the base of an undescribed or unknown population parameter. It is considered consistent, unbiased, and efficient. In other words, and the estimate should vary the least from sample to sample.

The point estimator technique is a technique that is used in statistics that comes into use to arrive at an estimated value of an unknown parameter of a population. Here, a single value or estimate is chosen from the sample set of data, which is generally considered the best guess or estimate from the lot. This single statistic represents the best estimate of the unknown parameter of the population.

• A point estimator is mainly utilized in statistics where a sample dataset is considered. A single best-judged value is selected, which provides the undescribed base or unknown population parameter.
• It is a technique used in statistics that comes into use to reach an estimated value of an unknown parameter of a population. 
• The characteristics of point estimators are bias, consistency, and the most efficient and unbiased.

Point Estimator Explained

Point estimators in statistics can help in finding approximate values of population parameters from some random samples. The sample that serves as the best estimate is used. The existing unrealistic methods is replaced by this method.

The point estimation method Point estimator solely depends on the researcher conducting the study on the method one needs to apply, as both point and interval estimators have pros and cons. However, it is a bit more efficient because it is considered more consistent and less biased. It can also be used when there is a change in sample sets.

Properties

The  properties of point estimators in statistics can be the following:

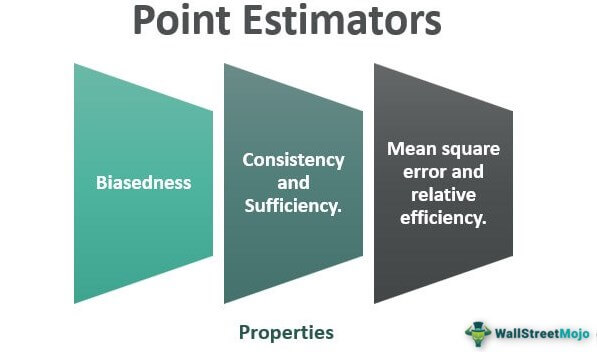
#1 - Bias

Biasness is the gap between the value expected from the estimator and the value of estimation considered regarding the parameter. When the estimated value shows zero bias, the situation is considered unbiased. Also, when the estimated value of the parameter and the parameter value estimate is equal, the estimation is considered biased. The closer the expected value of estimation to the measured parameter value, the lower the business level.

#2 - Consistency

It states that the estimator stays close to the parameter's value as the population's size increases. Thus, a large sample size is required to maintain its consistency level. When the expected value moves towards the parameter's value, we state that the estimation is consistent.

#3 - Most Efficient Or Unbiased

The most efficient estimator is considered the one which has the least unbiased and consistent variance among all the estimators considered. The variance considers how dispersed the estimator is from the estimate. The smallest variance should deviate the least when different samples are brought into place. But, of course, this also depends on the distribution of the population.

#4 - Mean Square Error And Relative Efficiency 

Lastly, mean square error and relative efficiency can be treated as properties. The mean square error is derived as the sum of the variance and the square of its bias. The estimator with the lowest MSE is considered to be the best.

Example

As an example of point estimator let us try to understand the below mentioned situation. The concept will be easy to understand with the help of an example. If we try to estimate the height of the people living in a region where total population is, suppose 5,000, it is quite difficult to get the height of each person individually. Thus the best way is to collect the height data of a sample group of people living in that region, say 1000 people. Then calculate an average of the heights of the samples collected, which is , point estimator for the population mean. This value can be used as the point estimator of the 5000 population. This example of point estimator explains the concept clearly.

How To Calculate?

There are generally two prime methods which are as follows:

#1 - Method of Moments

This point estimation method was first used and invented by the famous Russian mathematician Pafnuty Chebyshev in 1887. It generally applies to collecting facts about an entire population and applying the same facts to the sample set obtained from the population. It usually begins by deriving many equations related to the moments prevalent among the population and applying the same to the unknown parameter.

The next step is drawing a random sample from the population where one can estimate the moments. Then, the second step equation one can calculate using the mean or average of the population moments. It generally creates the best point estimator of the unknown set of parameters.

#2 - Maximum Likelihood Estimator

Here, the set of unknown parameters is derived in this technique, which can relate the related function and maximize the function. Here a well-known model is selected, and the values present are used further to compare with the data set, which on a trial and error method, helps us to adjourn the most relevant match for the data set, which is called the point estimator.

Advantages

• It is considered the best-chosen or the best-guessed value. It generally brings a lot of consistency to the study, even if the sample changes.
• Here, we generally focus on a single value, saving much study time.
• Point estimators are considered less biased and more consistent. Thus, its flexibility is generally more than interval estimators when there is a change in the sample set.

Disadvantages

• The process is not reliable.
• It is a time-consuming process. The analysis requires many members who can collect data is analyse them.
• It is suitabke for large projects or assignments.

Point Estimation Vs Interval Estimation

• The prime difference between the two is the value used.
• In point estimation, a single value is considered: the best statistic or the statistic means. In interval estimation, a range of numbers is considered to drive information about the sample set.
• Point estimators are generally estimated by moments and maximum likelihood, whereas interval estimators derive by techniques like inverting a test statistic, pivotal quantities, and Bayesian intervals.
• A point estimator will provide an inference related to a population by estimating a value related to an unknown parameter using a single value or point. In contrast, an interval estimator will provide an inference related to a population by estimating a value related to an unknown parameter using intervals.

Frequently Asked Questions (FAQs)

Recommended Articles

This article is a guide to the definition of Point Estimators. We explain it with example, how to calculate, properties & differences with interval estimation. You may learn more about financing from the following articles: -

• Kurtosis
• Harmonic Mean
• Geometric Mean
• Arithmetic Mean
• EWMA