Nash Equilibrium Game Theory

Nash equilibrium is a game theory concept that helps determine the optimum solution in a social situation (also called a non-cooperative game), wherein the participants are not incentivized to change their initial strategy. In other words, in this strategy, a participant doesn’t gain anything by diverging from their initial strategy, which is subject to the assumption that the other participants also don’t change their strategies.

Nash equilibrium and dominant strategy are two different instances. In the former case, participants refrain from switching to another option, which worked for fellow players, thinking the switch would lead to the worst outcome. On the contrary, in the latter situation, participants stick to the best outcome irrespective of what other people choose.

• Nash equilibrium is a game theory that helps find the optimum solution in a social situation (non-cooperative game) where the participants are not encouraged to change the initial strategy. 
• The Nash equilibrium game theory is named after American mathematician John Nash. He was awarded the Nobel Prize in Economics in 1994 for his invaluable contribution to game theory.
• Oskar Morgenstern and John von Neumann developed this mixed-strategy concept under Nash equilibrium in “The Theory of Games and Economic Behavior” (1944).

Nash Equilibrium in game theory is named after American mathematician John Nash, who was awarded the Nobel Prize in Economics in 1994 for his invaluable contribution to the field of game theory.

The underlying principle is similar to Antoine Augustin Cournot's oligopoly theory (1838). As per Cournot's theory, all the firms in a competitive market would choose to produce only that much output to maximize their profit. However, the best output of one firm is dependent on the output of the others in the market. Consequently, Cournot equilibrium is achieved only when each firm's output maximizes its profits, taking into account the output of the other firms, which is again the strategy for Nash equilibrium.

The modern concept of Nash equilibrium theory has changed a bit. It also includes mixed strategies, wherein the participants avert possible actions and prefer to choose probability distribution. Oskar Morgenstern and John von Neumann pioneered this mixed-strategy concept under Nash equilibrium in their book The Theory of Games and Economic Behavior (1944).

Let us have a look at the Nash equilibrium examples to know how to find the possibility of an outcome being the most favorable:

Example #1

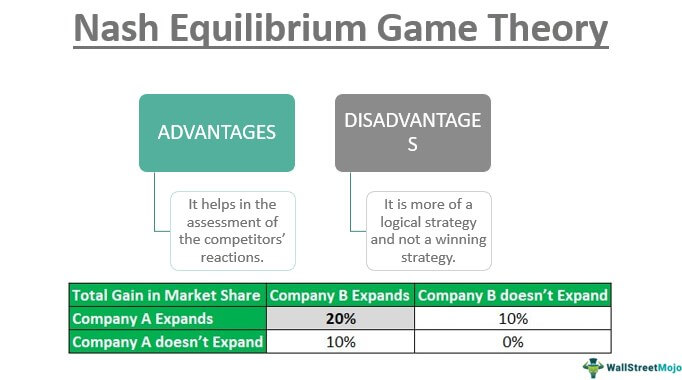
X Co. and Y Co. illustrate the concept of Nash equilibrium in game theory. Both companies intend to determine the right time to expand their production capacity. If both companies expand their capacities now, each can increase their market share by 10%. However, if only one of them decides to expand, it can increase its market share by 20%, while the other will not gain any market share. On the other hand, if both companies give up the idea of expansion, neither will gain any market share. The below table indicates the payoff in this case.

So, in this case, the Nash equilibrium is achieved when both companies expand their production capacities as it offers a better payoff overall.

Example #2

Let us look at another example to illustrate the concept of multiple Nash Equilibria in game theory. Imagine that two friends, David and Neil, are registering for a new semester. They both have the option to choose between finance and marketing. If David and Neil register for the same class, they can study together for the exams. But, on the other hand, if they pick different classes, they will neither lose out on the mutual benefit of group study. The below table indicates the payoff in this case.

So, in this case, multiple Nash equilibria are achieved when David and Neil register for the same class. Thus, the outcomes are David picks finance – Neil picks finance, and David picks marketing – Neil picks marketing.

• Analysis of hostile situations like arms races, and wars (Prisoner's dilemma).
• Analysis to mitigate conflict through repeated interactions.
• Study human behavior to determine when people with different preferences can cooperate.
• Determination of probability of currency crises and bank runs (Coordination game).
• Design algorithm for traffic control (Wardrop's principle).

Here are a few pros and cons of the concept one must know of to have better clarity of the Nash equilibrium definition:

Advantages

• It is a well-defined quantitative approach to decision-making in a competitive situation.
• It helps in the assessment of the competitors’ reactions.
• It is a management tool that helps in policy making.

Disadvantages

• Determining the optimal solution becomes difficult with the increase in participants.
• It is more of a logical strategy and not a winning strategy.
• The concept fails to account for uncertainties encountered in real-life business situations.
• The theory expects the participants to act rationally, which is not always the case.

This article has been a guide to what is Nash Equilibrium. Here we explain it with examples, applications, advantages, and disadvantages. You can learn more about it from the following article:  –

• Financial Engineering Career Guide
• Best Strategy Books
• Top 10 Best Pricing Books
• Best Economics Books