What are Mutually Exclusive Projects?
Mutually Exclusive Projects is the term which is used generally in the capital budgeting process where the companies choose a single project on the basis of certain parameters out of the set of the projects where acceptance of one project will lead to rejection of the other projects.
These projects are such that acceptance of project A will lead to rejection of project B. The projects, in this case, happen to compete with each other directly.
Methods used by Companies to Evaluate Mutually Exclusive Projects
There are various methods adopted by companies to evaluate mutually exclusive projects, and they serve as the criterion on which the acceptance or rejection decision shall be made.
#1 – NPV (Net Present Value)
NPV refers to the present value of the future cash flows arising out of the project, which then deducts the initial outlay or investment.
The decision criteria stand as follows:
- Accept if NPV > 0
- Reject if NPV < 0
#2 – IRR (Internal Rate of Return)
It is nothing but the discount rate that would make all of the present values of cash flows equal to the initial outlay. IRR is the discount rate at which the NPV of the project equals zero. Companies often have a hurdle rate or a required rate of return that serves as the benchmark.
The decision criteria therefore are :
- Accept if IRR > r (Required rate of return/hurdle rate).
- Reject if IRR < r (Required rate of return/hurdle rate).
#3 – Payback Period
The payback Period method takes into consideration the tenure or rather the number of years required to recover the initial investment based on the cash flows of the project.
#4 – Discounted Payback Period
One drawback of the payback period is that the cash flows do not consider the impact of the time value of money. Hence discounted payback period, therefore, considers the cash flows by discounting them to their present values and then calculating the payback.
#5 – Profitability Index (PI)
Profitability Index refers to the present values of the future cash flows arising out of the project, which is then divided by the initial investment.
4.9 (1,067 ratings) 250+ Courses | 40+ Projects | 1000+ Hours | Full Lifetime Access | Certificate of Completion
The investment criteria are :
- Invest if PI > 1
- Reject if PI < 1
Examples
Example #1
Consider the following cash flows of project A and project B.
| Year | Cash Flow – Project A | Cash Flow – Project B |
| 0 | -$660,000.00 | -$360,000.00 |
| 1 | $168,000.00 | $88,000.00 |
| 2 | $182,000.00 | $120,000.00 |
| 3 | $166,000.00 | $96,000.00 |
| 4 | $168,000.00 | $86,000.00 |
| 5 | $450,000.00 | $207,000.00 |
Solution:
Calculation of NPV for Project A will be –
Calculation of NPV for Project B will be –
The NPV and IRR calculation using an excel workbook is demonstrated asunder. Assuming a discount rate of 13%(future cash flows are discounted at 13% to arrive at their present value), using the NPV function, we are able to arrive at the required NPV after deducting the initial outlay. (Year zero in this case).
Calculation of IRR for Project A will be –
Similarly, IRR can now also be arrived at using the IRR function in excel, as demonstrated below.
Calculation of IRR for Project B will be –
NPV is positive in the case of both projects, and IRR is greater than the discount rate of 13%.
Since the projects are mutually exclusive, we can’t choose all the projects simultaneously. However, since both the NPV and IRR are greater in the case of project A, we would choose project A since these are mutually exclusive projects.
So have you come across scenarios wherein the NPV and IRR conflict against each other while evaluating such projects?
Yes, certainly, there are situations where we counter conflict between NPV and IRR while evaluating such projects.
Example #2
Consider the following cash flows of 2 projects.
| Year | Cash Flow – Project A | Cash Flow – Project B |
| 0 | -$500.00 | -$500.00 |
| 1 | $200.00 | $0.00 |
| 2 | $230.00 | $0.00 |
| 3 | $180.00 | $0.00 |
| 4 | $180.00 | $1,000.00 |
Solution:
The NPV and IRR assuming a discount rate of 10%, are displayed below as follows.
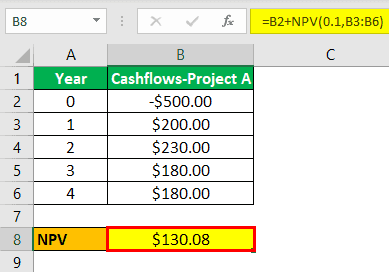
Calculation of NPV for Project A will be –
Calculation of NPV for Project B will be –
Calculation of IRR for Project A will be –
Calculation of IRR for Project B will be –
If you happen to notice, NPV of project B is greater than A, whereas the IRR of project A is greater than project B.
Please refer given excel template above for the detailed calculation of mutually exclusive project examples.
Does One Method Have an Advantage Over the Other?
- In instances where the initial cash flows are higher, it is noticed that the IRR shows a higher number, in contrast to the project where the project has cash flows coming in later. Hence IRR will tend to skew towards a higher range when there are higher cash flows initially.
- Usually, the discount rates change over the life of the company. An unrealistic assumption that IRR makes is that all cash flows in the future are invested at the IRR rate.
- There may also be instances wherein there are multiple IRRs or no IRR for a project.
Does NPV Seem Like a Better Option then IRR?
Well yes. An important assumption that NPV makes is that all future cash flows are reinvested at the most realistic discount rate-opportunity cost of funds. NPV, too, has its disadvantages as it does not consider the scale of a project.
Nevertheless, when faced with a conflict between IRR and NPV in the case of mutually exclusive projects, it is suggested to go ahead with the NPV method as this happens to show the amount of real wealth gain for the company.
Advantages and Disadvantages
Advantages
- The company will be able to optimally select the best project/investment that gives in the best returns.
- The company will be able to commit their capital only to the optimal project considering the limited resources.
Disadvantages
- Though both projects generate positive NPVs, companies will have to select the winner and leave out the rest.
Are There any Changes Off Late in Mutually Exclusive Projects?
- Well, yes, there is something called incremental analysis that is being undertaken when both projects seem feasible.
- It refers to an analysis of differential cash flows of the two projects (Smaller cash flows are deducted from the cash flows of the larger project).
- However, fret not like this analysis is not predominantly used, and companies do majorly rely on NPV and IRR analysis.
Conclusion
Well, I think to gauge on the feasibility or viability of the investments, these methods serve as a great decision-making tool for corporates, as when they invest in positive NPV generating mutually exclusive projects, they tend to add to the wealth of the shareholders, which no doubt gets reflected in the increasing share prices.
Recommended Articles
This has been a guide to What are Mutually Exclusive Projects and its definition. Here we discuss the examples of mutually exclusive projects and the best methods for evaluation. You can learn more about financial modeling from the following articles –
- 250+ Courses
- 40+ Projects
- 1000+ Hours
- Full Lifetime Access
- Certificate of Completion
