Table Of Contents
Mutually Exclusive Events Definition
Mutually exclusive events cannot occur simultaneously. Hence, the probability of two mutually exclusive events occurring at the same time is zero. For instance, the result of an exam can either be pass or fail, but never both.
This statistics concept is crucial for the capital budgeting process where companies choose a single project based on certain parameters. Out of many projects, the acceptance of one will lead to the rejection of others. The projects, in this case, directly compete with each other.
Key Takeaways
- A mutually exclusive or disjoint event is a situation where the happening of one event causes the non-occurrence of the other. Though these outcomes are not independent, there exists a negative relationship in their occurrences.
- Two events A and B, are said to disjoint if P(A∩B) = 0, and P(A∪B) = P(A)+P(B).
- Every disjoint event holds an opportunity cost of not selecting the other.
- It is an essential and frequently used phenomenon in finance, investment, capital budgeting, comparison of projects, and comparison of returns.
Understanding Mutually Exclusive Events
In probability theory, mutually exclusive events are also called disjoint events. Disjoint events are the two or more outcomes that cannot crop up together—in such a situation, the happening of one event results in the non-occurrence of the others. For example, if you have to be home but you have an office that day, both events become mutually exclusive. Like if you are going to the office, you cannot be at home and vice versa. When two events can’t happen at the same time, then their probability will also be zero. Disjoint events are not independent of each other.
In finance, analysis of disjoint events facilitates crucial decision-making like selecting an investment opportunity or capital budgeting. The time value of money comes into play when one has to choose between mutually exclusive investment options or business projects. Time value of money refers to the concept where money received in the present is of higher worth than money to be received in the future. This is because the money received now can be invested and can generate cash flows, this ultimately leads to future enterprise. The mutual exclusivity concept helps analysts figure out the time value of each option.
Also, every disjoint event has a specific opportunity cost resulting from the non-happening of its counterpart. For example, a board of directors chose business expansion over equity investment. In doing so, they grab one of the options but also lose the other.
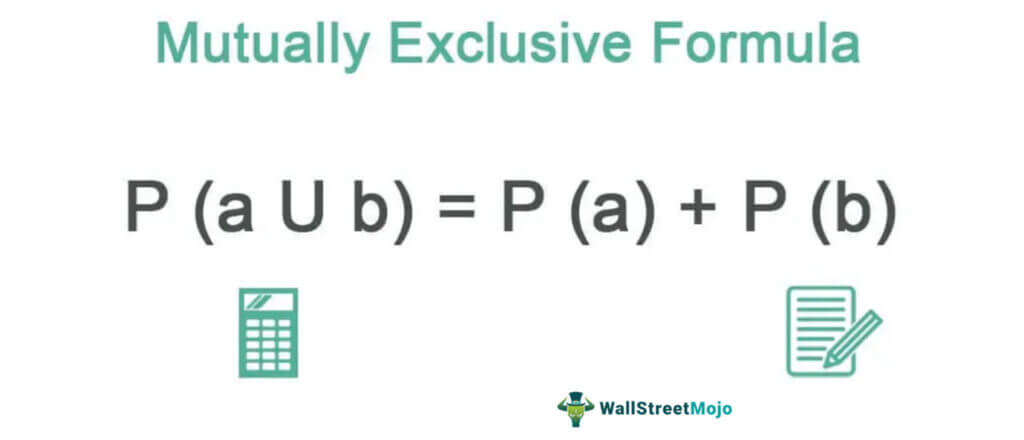
Mutually Exclusive Events Formula
The probability of attaining mutual exclusivity is the sum of the probabilities of both events. Given below is the formula to compute the same:
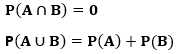
Here,
- P(A∩B) is the probability of integration of A and B;
- P(A∪B) is the probability of A and B’s union;
- P (A) = Probability of A;
- P (B) = Probability of B.
Mutually Exclusive Probability
In this section, we will understand the above formula in detail. To prove mutual exclusivity of two or more events, we need to go through the following probability rules:
- Multiplication Rule: The most straightforward method is to determine the joint probability or integration of two or more events. If the answer is zero, then it means that these events cannot take place simultaneously. Thus, P(A∩B) = 0 shows that these events are disjoint from each other.
- Addition Rule: Alternatively, the individual probabilities of the events can be added up. This results in the probable occurrence of one possibility out of many. It is denoted as P(A∪B) = P(A)+P(B).
Mutually Exclusive Events Examples
Example #1 - For P (A and B) = 0
Let us assume that Jennifer is planning for a tour. She has two choices Italy and Istanbul. When calculating the cost, she realizes she cannot afford both. Hence, she has to choose one among them. If she wants to visit Istanbul, she cannot afford Italy and vice versa.
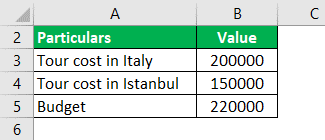
- Here, cost to tour Italy = Rs. 2, 00, 000
- Cost to Istanbul = Rs. 1, 50, 000
- And your budget = Rs. 2, 20, 000
Solution:
Use the below data for calculation of Mutual Exclusivity.
Calculation of Disjoint Events can be done as follows:
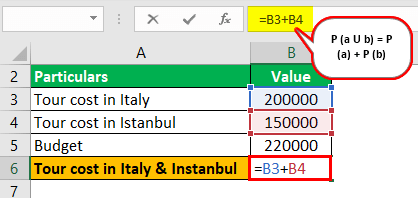
Tour cost in Italy & Istanbul = 2, 00,000 + 1, 50,000
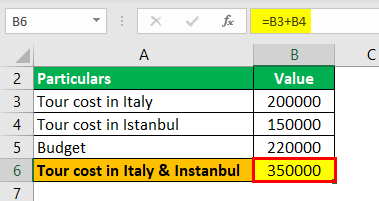
Tour cost in Italy & Istanbul = 350000 (0 mutually exclusive as she can’t visit both simultaneously as her budget is only 220000).
Example #2 - For P (A U B) = P (A) +P (B)
A final handball match is arranged between two teams England and India. 1000 people from the audience were asked to vote for the team that would win the game. The audience voted as follows:

Solution:
The calculation can be done as follows:
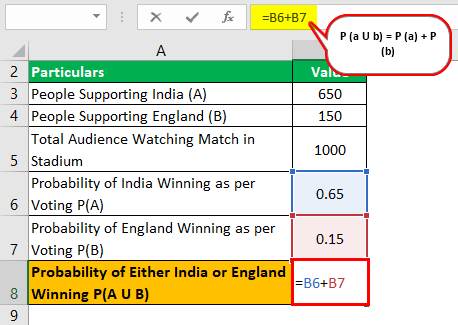
- Probability of India winning the match (A) = 650/1000 =0.65
- Probability of England winning the match (B) = 150/1000=0.15
- Probability of match becoming draw P (A ∩ B) = 0 (there won’t be a draw)
P (A U B) = P (A) + P (B)
P (A U B) = 0.65 + 0.15
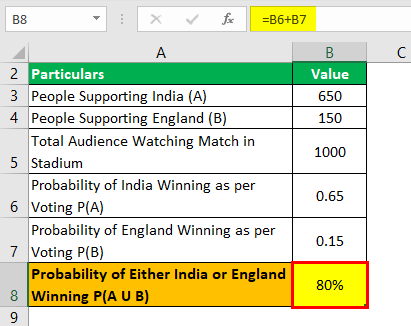
P (A U B) = 80%
Mutually Exclusive Events vs. Independent Events
Mutually exclusivity of events is not the same as independent events. For mutual exclusivity, the occurrence of one event is dependent upon the non-occurrence of the other. Whereas independent events refer to those outcomes which are not related, and the happening of one doesn’t impact the occurrence of the other. Moreover, unlike mutual exclusivity, the outcomes for independent events can appear simultaneously.
For instance, if a person is late to a railway station, he will either catch or miss the train. Thus, both these events are exclusive, and only one can happen. On the contrary, the probability of a music album being a hit and the probability of a movie’s failure are two independent events that can occur parallelly.
