Midrange Formula

Formula to Calculate Midrange of a Number

The midrange formula calculates the middle value of the two numbers given. According to the formula, the given two numbers add, and the resultant divides by 2 to get the midpoint value of the two.

The midrange is the middle point of a range of numbers. The mid-range of a series of numbers will be the average of the highest and lowest numbers. For example, if a series of numbers has 10 observations, the highest point is 250, and the lowest point is 50. So then, the range for that observation will be from 50 to 250.

Midrange = (Highest Value+ Lowest Value)/2

Examples

Example #1

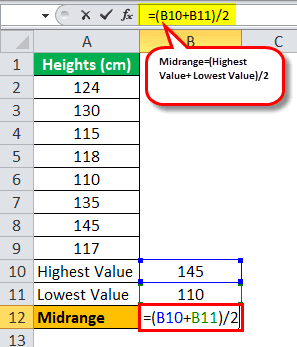
Let us try to find out how to calculate the midrange with the help of an example. Let us analyze the height of a class of 8 students in centimeters. Suppose the heights of each student in the class are 124, 130, 115, 118, 110, 135, 145, and 117. To calculate this for the whole population, we need to find the highest and lowest values of the observed values.

Solution:

Use the following data for the calculation:

The highest value of the observed heights will be-

Highest Value = 145

The lowest value of the observed heights will be:

Lowest Value=110

So, the calculation of the midrange can be as follows:

= (145+110)/2

The example shows that the midrange for the observed value is 127.5 centimeters.

Example #2

Let us try to find out how to calculate the midrange with the help of another example. Let us analyze the weight of a class of 8 students in kilograms. Suppose the weights of each student in the class are 45, 49, 54, 60, 42, 65, 56, and 59. To calculate this for the whole population, we need to find the highest and lowest values of the observed values.

Solution:

Use the following data for the calculation of the midrange.

The highest value of the observed weights will be-

Highest Value =65

The lowest value of the observed weights will be-

Lowest Value = 42

So, the calculation of the midrange is as follows:

= (65+42)/2

The example shows that the midrange for the observed value is 53.5 kilograms.

Example #3

Let us try to find out how to calculate the midrange with the help of another example. Let us analyze the price of a series of Samsung phones sold in a store. Suppose the price of a range of Samsung phones are $160, $168, $185, $195, $115, $186, $125 and $150. To calculate this for the whole population, we need to find the highest and lowest values of the observed values.

Solution:

Use the following data for the calculation of the midrange.

The highest value of the observed prices will be-

Highest Value =195

The lowest value of the observed prices will be-

Lowest Value =115

So, the calculation can be as follows:

= (195+115)/2

Relevance and Use of Midrange Formula

The midrange formula is relevant in practical life. Like the mobile example we discussed above, a company has a range of phones with various price points at any time. So, with the help of finding out the mid-range of the series of phones, one can determine whether the particular model of the phone he is looking for is above the average price or below the average price. Likewise, if we find out the midrange of the weights of a class of students, then by having that, we can guess whether a particular student is overweight or underweight in that class. Pro tip: After understanding the calculation of midrange by formula, then you can use a midrange calculator and ensure your final answer with ease.

Frequently Asked Questions (FAQs)