Method Of Moments

What Is The Method Of Moments (MoM)?

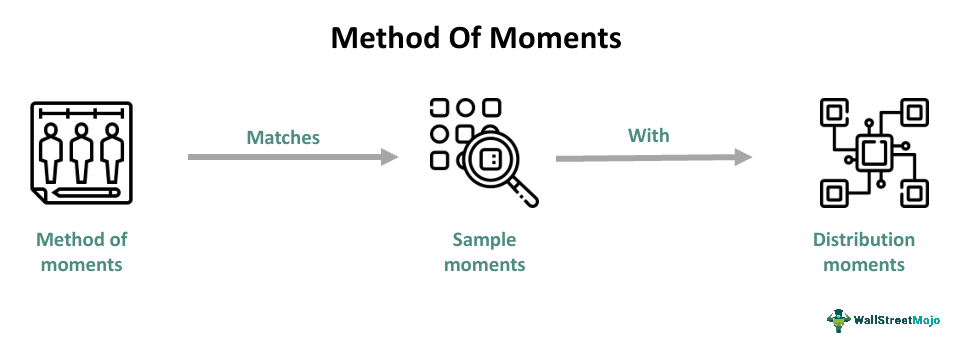
The Method of Moments (MOM) is a technique used to estimate parameters by matching sample moments with distribution moments to construct estimators. It assumes that the sample moments are good estimates of the corresponding population moments. The concept is used in various fields, including statistics.

The method gets its name from taking moments using appropriate weighing functions and integration. Similar to quantiles, moments are parametrized characteristics of the distribution of random variables. They are parameterized by natural numbers and provide complete characters of the distribution. They can solve equations in numerical analysis, such as differential or integral equations.

• The method of moments (MoM) is a technique that estimates parameters by equating sample moments with distribution moments and creating estimators.
• Pafnuty Chebyshev introduced the method in 1887 as part of the proof of the central limit theorem.
• The method of moments starts by expressing the population moments, which are the expected values of the random variable's powers, as functions of the parameters of the required ones. These expressions are then equated to the sample moments.
• While this method is simple, the derivation can be lengthy, and it does not provide full distribution.

Method Of Moments Explained

The method of moments in statistics is a technique of estimation of population parameters by comparing and matching sample moments with theoretical moments. This method was put forward by Pafnuty Chebyshev in 1887 with the aim of proving the central limit theorem. The method begins with the expression of the population moments. These are the expected values of the random variable's powers as functions of the parameters of the required ones. These expressions are then equated to the sample moments. The number of equations equals the number of parameters that need estimation. One can obtain estimates for the parameters by solving these equations.

The unknown function is roughly represented using a finite series of known expansion functions and unknown expansion coefficients. Afterwards, the approximate equation that results from substituting the approximation function into the original operator equation is checked to verify that the weighted residual is zero. The unknown coefficients are then expressed in many simultaneous algebraic equations. One usually uses matrix calculus in solving these equations. In general, it is simple to identify MoM estimators. Additionally, they exhibit general consistency. Moreover, it is a qualitative definition denoting that the estimator's convergence to the parameter's real value as the sample size increases.

The Method of Moments takes place in two steps. First, it matches sample moments, calculated from data, with theoretical moments using equations. Second, it solves these equations to estimate the probability distribution parameters. One can approximately solve the equations involving linear operators, such as differential or integral equations, using the method of moments.

Assumptions

The main assumption is that the sample equivalents will converge to the expected value through the application of the law of large numbers. It is the case the expected value of population moments is known (such as variance or mean). The criteria using these moment limitations is if the moments are functions of the parameters that are required to be estimated.

The approach yields dependable estimates if the sample size is large enough and hence is another key assumption. Similarly, it is necessary to use well-defined and finite sample moments to arrive at the results.

Examples

Let us look into a few hypothetical examples to understand the concept better.

Example #1

Suppose Dan, a researcher, wants to estimate the variance and mean of a continuous random variable representing the income of adults. He collects a random income sample and uses the method of moments to equate the sample mean and variance with the corresponding population moments to estimate the parameters. He used a method of moments calculator to arrive at the results. The results from the study could help him give government data to make crucial economic policy decisions.

Example #2

Suppose Anne, an investor, uses MOM to find the value of an investment. The MOM can be used to estimate the parameters of asset return distributions. She can estimate the mean and volatility of the asset returns through this by equating the sample moments of returns with the moments of a specific distribution (such as the normal distribution). It helped him in making wise investment choices. She used MOM calculator to arrive at the results.

Applications

The method of moments is a statistical technique that widely finds application in system design, signal processing, and communications. It helps estimate parameters in statistical models. MOM is an important tool in engineering that provides insights into various mathematical models.

Advantages And Disadvantages

Some of its advantages and disadvantages are as follows:

Advantages

• It simplifies a theoretically infinite number of mass balance equations to a smaller and more manageable set.
• The derivation process of MOM is straightforward. 

Disadvantages

• It does not provide a prediction of the full distribution. 
• It does not account for the dependence of reaction rate constants on chain length.
• Although the derivation is simple, the process can be lengthy, which may initially be confusing.

Method Of Moments vs Finite Element Method (FEM)

The differences between both the concepts are as follows:

• The FEM is a general method for solving partial differential equations using two or three space variables. The method subdivides a large data system into smaller, simpler parts called finite elements to solve a problem. On the other hand, one uses the method of moments in statistics to calculate population parameters and higher moments like skewness and kurtosis.
• MoM in engineering solves the surface integrals related to the aperture field elements. On the other hand, the FEM finds application in solving electromagnetic fields inside the enclosure.
• FEM uses sparse matrixes, while MoM uses the full matrixes.

Frequently Asked Questions (FAQs)

Recommended Articles

This article has been a guide to what is Method Of Moments. We explain its examples, assumptions, advantages, applications, & comparison with finite element method. You may also find some useful articles here -

• Generalized Method of Moments 
• Spatial Autoregressive Model
• Weibull Distribution