Mean Examples

Publication Date :

22 May, 2019

Blog Author :

Edited by :

Reviewed by :

Table Of Contents

Examples of Mean

Mean is the most commonly used measure of central tendency. There are many examples of mean that one can calculate based on the availability and requirement of data: arithmetic mean, weighted mean, geometric mean, and harmonic mean.

Examples of Mean

Mean is the most commonly used central tendency tool.
One can calculate several mean examples based on the availability and requirement of data: arithmetic mean, weighted mean, geometric mean, and harmonic mean.
One may use the arithmetic mean to estimate if there is no weight for each value or factor.
Its primary disadvantage is that it is sensitive to extreme values, especially if we have a smaller sample size. It is not suitable for skewed distribution.

Top 4 Examples of Mean

Example #1 - Arithmetic Mean

Suppose a set of data containing the following numbers:

8, 16, 15, 17, 18, 20, 25

We have to calculate the mean for the above set.

Solution:

Arithmetic Mean = Sum of Total Numbers / Number of Values

So, the calculation of arithmetic mean will be –

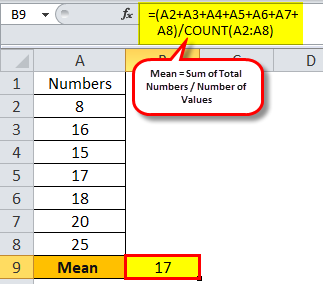
In this case it will be (8 + 16 + 15 + 17 + 18 + 20 + 25)/7 which comes to 17.

Mean = 17

It means the simple arithmetic mean as none of the data in the sample are repeating, i.e., ungrouped data.

Example #2 - Weighted Average Mean

In the above, all the numbers gave an equal weight of 1/7. Suppose all the values have different weights. Then the mean will be pulled by the weight.

Suppose Fin wants to buy a camera, and he will decide among the available option based on their features as per the following weights:

Battery Life 30 %
Image Quality 50 %
Zoom Range 20 %

He is confused about the two available options:

Option 1: The Canon camera gets 8 points for image quality, 6 points for battery life, and 7 points for the zoom range.
Option 2: The Nikon camera gets 9 points for image quality, 4 points for battery life, and 6 points for zoom range.

Which camera should he go for? The above points are on 10-point ratings.

Solution:

The calculation of the total weighted average for Canon will be:

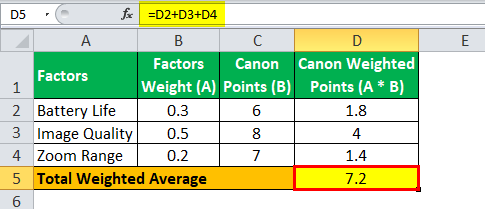
Total Weighted Average = 7.2

The calculation of the total weighted average for Nikon will be –

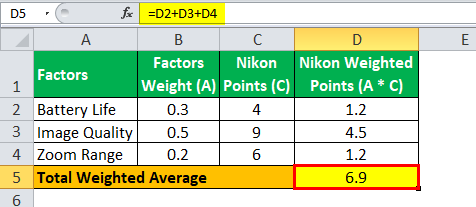
Total Weighted Average =6.9

We cannot calculate the mean of the points for the solution as weights are there for all the factors.

Based on Fin's weighting factor, one can recommend that he go for the Canon camera as its weighted average is more.

Example #3 - Geometric Mean

This method of mean calculation is usually for growth rates like population or interest rates. On the one hand, arithmetic means adding items, whereas geometric mean multiplies items.

Calculate the geometric mean of 2, 3, and 6.

Solution:

One can calculate it using the formula of geometric mean, which is:

Geometric Mean ( X )= ^N√(X₁*X₂*X³………….X_N)

So geometric mean will be -

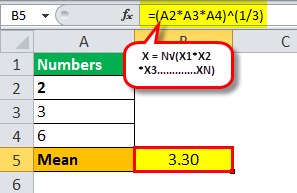
=(2 * 3 * 6)^1/3

Mean = 3.30

Calculate the geometric mean for following a set of data:

1/2, 1/5, 1/4, 9/72, 7/4

So, the geometric mean will be:

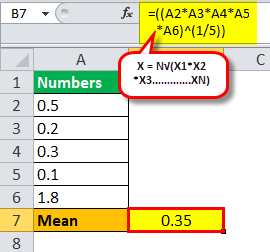
One can calculate it as follows:

(1/2 * 1/5 * 1/4 * 9/72 * 7/4)^1/5

Mean = 0.35

Suppose Fin's salary jumped from $2,500 to $5,000 over ten years. Then, using the geometric mean, calculate his average yearly increase.

So, the calculation of the geometric mean will be:

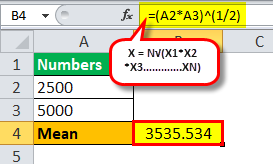
=(2500 * 5000)^1/2

Mean = 3535.534

The above mean is the increase over 10 years. Therefore, the average increase over 10 years will be 3535.534/10, i.e., 353.53

Example #4 - Harmonic Mean

The harmonic mean is another numerical average calculated by dividing the number of observations available by the reciprocal of each number present in the series. So, the short harmonic mean is the reciprocal of the arithmetic mean of reciprocals.

Let us take an example of two firms in the market: High International Ltd. and Low International Ltd. High International Ltd. has a $50 billion market capitalization and $2 billion in earnings. On the other hand, Low International Ltd. has a $0.5 billion market capitalization and $2 million in earnings. Suppose one index is made by considering the stocks of the two companies High International Ltd. and Low international Ltd., with the 20% amount invested in High International Ltd. The remaining 80% amount is invested in Low International Ltd.

Calculate the PE ratio of the stock index.

Solution:

The P/E ratio of the two companies will be calculated first to calculate the PE ratio of the index.

P/E Ratio = Market Capitalization/ Earnings

So, the calculation of the P/E ratio for High International Ltd. will be as follows:

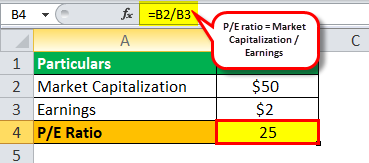
P/E ratio (High International Ltd.) = $50 / $2 billion

P/E Ratio (High International Ltd.) = $25 billion.

So, the calculation of the weighted arithmetic mean will be:

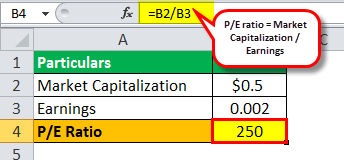
P/E ratio (Low International Ltd.) = $0.5/$ 0.002 billion

P/E ratio (Low International Ltd.)= $250

Calculation of the P/E ratio of the index using:

#1 - Weighted Arithmetic Mean:

Weighted Arithmetic Mean = (Weight of investment in High International Ltd. * P/E ratio of High International Ltd.) + (Weight of investment in Low International Ltd. * P/E ratio of Low International Ltd.)

So, the calculation of the weighted arithmetic mean will be:

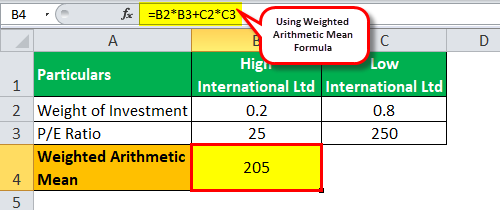
Weighted Arithmetic Mean = 0.2 * 25 + 0.8 * 250

Weighted Arithmetic Mean = 205

#2 - Weighted Harmonic Mean:

Weighted Harmonic Mean = (Weight of investment in High International Ltd. + Weight of investment in Low International Ltd.) /

So, the calculation of the weighted harmonic mean will be:

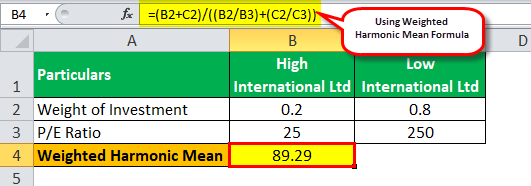
Weighted Harmonic Mean = (0.2 + 0.8) / (0.2/25 + 0.8/250)

Weighted Harmonic Mean = 89.29

From the above, one can observe that the weighted arithmetic mean of the data significantly overestimates the price-earnings ratio mean calculated.

Conclusion

The arithmetic mean can be used to calculate the average if there is no weight for each value or factor. Its major disadvantage is that it is sensitive to extreme values, especially if we have a smaller sample size. It is not at all appropriate for skewed distribution.
A geometric mean method is when a value changes exponentially. The geometric mean cannot be used in any of the values in the data is zero or less than zero.
The harmonic mean is used when small items have to be given greater weight. It is suitable for calculating the average rate, time, ratios, etc. Like the geometric mean, sample fluctuations do not affect the harmonic mean.

Frequently Asked Questions (FAQs)

How to find the arithmetic mean examples?

The arithmetic mean examples refer to the sum of all group numbers when divided by the number of items in that list

What is cancel culture mean examples?

Cancel culture is also known as call-out culture. It is a phrase contemporary to the late 2010s and early 2020s that refers to a culture where those deemed to have acted or spoken unacceptably are ostracized, boycotted, or shunned.

Can the mean be used with categorical or qualitative data?

The mean is typically used with numerical or quantitative data. Other measures like mode or proportions are more appropriate for categorical or qualitative data, such as categories or groups.

Can the mean be calculated for skewed distributions?

Yes, the mean can be calculated for skewed distributions. However, it may not accurately represent the typical values in the dataset if the distribution is highly uneven. Other measures like the median or transformations better represent the central tendency in such cases.