Mean

Mean in statistics refers to the average of a collection of values. The collection of values can be two or more. It is a measure of central tendency and output typical value in a collection or set of data.

In its simplest form, it is the mathematical average derived by adding the values given in a set and dividing it by the number of values in the set. In finance and probability, a similar concept is known as expected value, a synonym of mean or average value.

• Mean refers to the average of values or items in a given set. In its simplest form, it is derived by adding the values given in a set and dividing it by the number of values in the set.
• Mean is a central tendency measure. It is also known as the mathematical average or expected value.
• The main types are arithmetic, geometric, harmonic, root mean square, and contra harmonic. Each type primarily differs by the formula used.
• Its application is substantial in statistics and data analysis.
• Example: The average of numbers 1, 3, 5, and 3 will be (1+3+5+3)/4, which is equal to 3.

The mean is one of the simple methods employed in descriptive statistics used to interpret or summarize the given data set and derive relevant information or conclusion about the population or sample of a population represented by the data set. Most of the time, it is imperative to derive an average to understand the overall performance and simplify the statistical calculations.

It is also combined with the other central tendency measures like mode and median. These three central tendency measures are equal for a frequency distribution with a symmetrical frequency curve. In the case of a positively skewed distribution curve, the mean is greater than the median, and the median is greater than the mode. When the frequency distribution is negatively skewed, the mode is greater than the median, and the median is greater than the mean.

Fundamentally, it is the value obtained by dividing the sum of all observations by the number of observations. The Greek letter μ denotes the population means, and X̄ is the symbol for the sample mean.

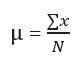
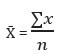
• ∑x: Sum of all observations or data values
• X̄: Number of observations in the population (population size)
• N: Number of observations in the sample (sample size)

Suppose, if a batch of nine people participated in a maths test; each student scored different marks out of 100 as given below:

The average mark is:

Sum of all the observations/total number of observations

= 522/9

= 58

So, 58 is the average mark.

Let's look into the brief description of a few significant types:

Arithmetic Mean (AM)

Arithmetic Mean is also referred to as the arithmetic average. It is calculated by summing all the observations and then dividing it by the total number of observations.

Geometric Mean (GM)

Geometric Mean involves finding the product of all observations or values and calculating the n^th root of the product of the observations. The value of n indicates the total number of observations. GM's calculation method is complex compared to AM, and GM is generally less than the AM. GM is commonly used in investment scenarios and is favorable when the observations in the sample exhibit dependence and significant fluctuations.

Harmonic Mean (HM)

Harmonic Mean formula and approach are quite different from other averages as the total number of observations or values are divided by the sum of the reciprocal of each observation or value in the set. It is one of the three classical Pythagorean means; the other two are AM and GM.

Root Mean Square (RMS)

The Root Mean Square calculation starts with finding the AM of squares of the values in the set. Then the square root of the mean square obtained gives the RMS value.

Contraharmonic Mean

It is complementary to the HM. It is calculated by dividing AM of squares of the values by the AM of the values.

• Its use is integral in experiments, statistics, and data analysis. For example, it is used in statistical testing, academic studies, geographical studies, and agricultural experiments.
• Traders and investors derive meaningful information by calculating average returns based on proper context, forming an important input to investment decisions.
• It is used in the calculation of dispersion and skewness.
• It can be applied to complete a simple time-series data if any one of the data points is missing.
• Examples of its application include a quasi-arithmetic mean-based filter for topology optimization and AM filter used for noise reduction.

This has been a Guide to Mean in Statistics and its definition. We explain its types, examples, synonyms & applications. You can learn more about accounting from the articles below –

• Trimmed Mean
• Mean vs Median
• Sample Mean vs Population Mean