Table Of Contents
What Is The Marginal Rate Of Technical Substitution (MRTS)?
The Marginal Rate of Technical Substitution (MRTS) is an economic concept that measures the rate at which one input can be substituted for another while keeping the level of output constant. The purpose of the Marginal Rate of Technical Substitution is to analyze the efficiency and optimal allocation of resources in production processes.
By understanding how inputs can be substituted, businesses can make informed decisions regarding the most cost-effective combination of inputs to maximize output. The importance of the MRTS lies in its ability to guide decision-making in production processes. It represents the slope of the isoquant curve, which depicts various combinations of inputs that produce the same output level.
Table of contents
- The Marginal Rate of Technical Substitution (MRTS) measures how easily one input can be substituted for another in the production process while keeping output constant.
- The MRTS helps firms determine the optimal combination of inputs to achieve higher efficiency and productivity.
- A diminishing MRTS indicates decreasing substitutability between inputs, while an increasing MRTS suggests higher substitutability.
- Understanding the MRTS is crucial for firms to make informed decisions regarding resource allocation, cost minimization, and production optimization. Given their production constraints, they can identify the most efficient way to allocate inputs and maximize output.
Marginal Rate Of Technical Substitution Explained
The Marginal Rate of Technical Substitution (MRTS) measures the rate at which one input can be substituted for another input while keeping the level of output constant. It represents the slope of an isoquant curve, which illustrates different combinations of inputs that yield the same level of output.
It helps firms determine the optimal mix of inputs, considering factors such as input prices and production requirements. Additionally, the MRTS plays a crucial role in the study of technological progress and innovation. It allows economists to assess the possibilities and limitations of substituting different inputs to improve productivity and efficiency in various industries. Overall, the Marginal Rate of Technical Substitution is a valuable tool for understanding an economy's resource allocation and production possibilities. It enables firms to make informed decisions, optimize their production processes, and achieve higher levels of efficiency.
Formula
The formula for the Marginal Rate of Technical Substitution (MRTS) is:
MRTS = ΔQ/ΔL divided by ΔQ/ΔK
Where:
- MRTS is the Marginal Rate of Technical Substitution.
- ΔQ/ΔL represents the change in output (Q) divided by the change in labor (L) quantity.
- ΔQ/ΔK represents the change in output (Q) divided by the change in capital (K) quantity.
This formula calculates the rate at which one input (labor) can be substituted for another input (capital) while maintaining the same level of output. In addition, it quantifies the slope of the isoquant curve, indicating how much of one input can be reduced as the other input is increased.
By calculating the MRTS, firms can determine the efficiency of their input allocation and make informed decisions about the optimal combination of inputs for a given output level. The MRTS varies along the isoquant curve, reflecting inputs' diminishing or increasing substitutability as more of one input is used relative to the other.
Examples
Let us have a look at the examples to understand the concept better.
Example #1
Consider a bakery that produces bread using two inputs: labor and capital. The bakery can allocate its resources by hiring workers and investing in machinery. Let's say the bakery wants to determine the optimal combination of labor and capital to produce a certain level of output.
Initially, the bakery employs 10 workers and uses 5 units of capital. At this point, the MRTS of labor for capital is 2, indicating that the bakery needs to hire 2 more workers for each additional unit of capital to maintain the same output level. This implies that labor is relatively more substitutable for capital.
Let's assume the bakery wants to increase its output without changing its total cost. So it decides to reduce capital to 3 units while hiring 14 workers. As a result, the MRTS of labor for capital increases to 4, indicating that labor has become even more substitutable for capital. By reallocating its resources, the bakery has found a more efficient combination of inputs to achieve higher output without increasing costs.
Example #2
Consider a car manufacturing company using labor and machinery inputs. The company wants to determine the optimal combination of labor and machinery to produce a certain number of cars.
Initially, the company employed 100 workers and had 10 machines. At this point, the MRTS of labor for machinery is 10, indicating that for each additional machine added, the company needs to hire 10 more workers to maintain the same level of car production. Suppose the company decides to reduce the number of machines to 5 and increase the number of workers to 150. As a result, the MRTS of labor for machinery decreases to 30, implying that labor is becoming less substitutable for machinery.
Graph
Let us look at the below-given chart. It illustrates a situation where a firm moves from point (a) to point (b) and employs an additional labor unit.
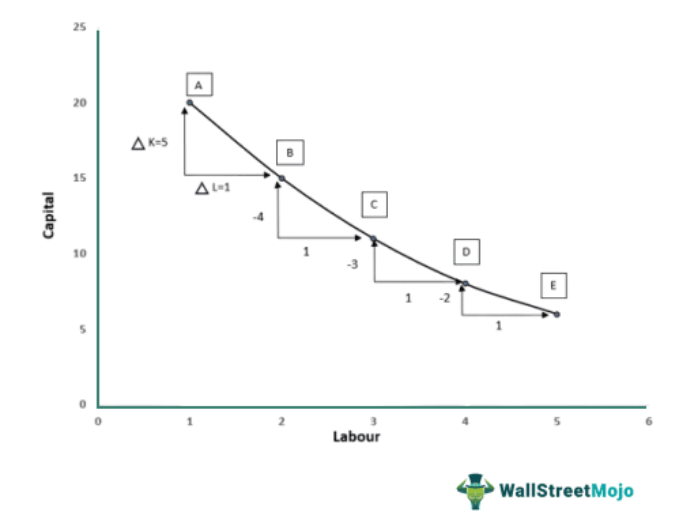
Despite reducing its capital (K) by 5 units, the firm remains on the same isoquant at point (b). Consequently, the Marginal Rate of Technical Substitution (MRTS) is determined to be 5. Furthermore, if the firm hires another unit of labor and progresses from point (b) to point (c), it can decrease its use of capital (K) by 4 units while remaining on the same isoquant. In this case, the MRTS is calculated to be 4.
Marginal Rate Of Substitution vs Marginal Rate Of Technical Substitution
Let us look at the differences between the Marginal Rate of Substitution and the Marginal Rate of Technical Substitution, they may seem similar but are not.
| Parameters | Marginal Rate of Technical Substitution (MRTS) | Marginal Rate of Substitution (MRS) |
|---|---|---|
| Definition | Measures the rate of input substitution in production | Measures the rate of substitution between goods |
| Application | Production and resource allocation | Consumer Choice and utility maximization |
| Inputs | Typically measures the substitution of production inputs, such as labor and capital. | Measures the substitution of goods or consumption items |
| Focus | Efficiency and optimal input combination | Consumer Preferences and utility maximization |
| Graphical representation | Isoquant curve | Indifference curve |
Frequently Asked Questions (FAQs)
A higher MRTS value suggests greater flexibility in substituting inputs. The Marginal Rate of Technical Substitution (MRTS) indicates how easily one input can be replaced with another while maintaining the same level of output. It helps assess the substitutability and efficiency of inputs in production.
A diminishing Marginal Rate of Technical Substitution refers to a situation where the rate at which one input can be substituted for another decreases as more of that input is substituted. It indicates a decrease in the ease of substituting inputs in the production process.
The slope of (MRTS) is a crucial measure that quantifies the trade-off between two inputs in the production process. A steeper slope indicates a higher substitution rate between inputs, implying that another can easily replace one input. Conversely, a flatter slope suggests a lower substitution rate, indicating that inputs are less easily substitutable.
No, the Marginal Rate of Technical Substitution (MRTS) cannot be negative. It represents the rate at which one input can be substituted for another, and by convention, it is always expressed as a positive value.
Recommended Articles
This article has been a guide to what is Marginal Rate Of Technical Substitution. We explain it with its formula, examples, and a graph. You may also find some useful articles here -
