Law Of Total Probability

Published on :

21 Aug, 2024

Blog Author :

Edited by :

Reviewed by :

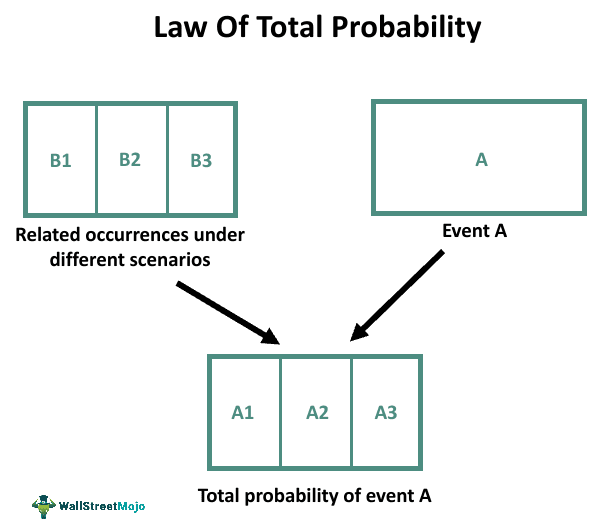
The Law of Total Probability refers to the possibilities or chances of an event to occur, by studying the frequency of its occurrence under various scenarios. It aims to calculate conditional probabilities, account for multiple conditions, study Bayesian inference and identify decision-making processes for figuring out the total probability of an event.

It is utilized in modeling and analyzing complex systems having numerous conditions or factors impacting the outcomes. The law finds use in confidence intervals, hypothesis testing and decision trees, Naive Bayes classifiers in machine learning, and spam filters and recommendation engines in artificial learning. It is helpful in making decisions in different fields like finance, economics, and mathematics.

What Is the Law of Total Probability?

The law of total probability states that the probability of an event A is determined by considering the likelihood of it happening under different circumstances.
Its purpose is to compute conditional probabilities, accommodate various conditions, apply Bayesian inference, and support decision-making regarding an event.
The formula for the law of total probability is as follows: P(A) = P(E1)P(A/E1) + P(E2)P(A/E2) + ... + P(En)P(A/En).
It finds use in decision analysis, risk assessment, reliability engineering, and queuing theory to calculate the posterior probability of hypotheses, evaluate risk, design reliable systems, and analyze performance measures.

Law Of Total Probability Explained

The law of total probability states that the probability of a particular outcome in different financial scenarios can be found by summing up all the individual probability scenarios weighted by the likelihood of each scenario. It is a fundamental probability theory concept allowing calculation of the probability of occurrence of an event by considering all related ways of it happening. It can be expressed for an event A and its related occurrence events B₁, B₂, ..., Bₙ mathematically as:

P(A) = P(A|B₁) * P(B₁) + P(A|B₂) * P(B₂) + ... + P(A|Bₙ) * P(Bₙ)

It works by breaking down the calculation of the probability of event A into smaller parts, considering how it can occur. One can denote all the possible scenarios of its occurrence by mutually exclusive events B1, B2, ..., Bn. After that, the probability of A given in each scenario is calculated. Then, these probabilities are weighted by corresponding probabilities of every scenario of occurrence, namely . Finally, one can calculate the overall probability of event A.

It works in finance in the following manner:

Identifies events: Identifying events making up portfolios return.
Calculates probabilities: Finding the probability of occurrence of stock returns and market returns.
Applies the law: The formula can calculate the probability of the entire portfolio return above the benchmark.

In finance, it has various implications like- managing and mitigating risk portfolio returns within a certain range. It can also be used to determine the best maximum asset allocation for a portfolio based on probabilities of various asset types. These asset classes give returns more than a certain benchmark. It helps in calculating hedging and pricing derivatives. Therefore, the law of total probability is essential in finance, enabling accurate probability calculations for risk management and decision-making.

Formula

Assuming a set of exhaustive events,

En = E1, E2, E3, ..., En

which together covers the entire sample space S. Also, these events are mutually exclusive. It means that the occurrence of one event does not affect the occurrence of others and has no common elements:

sample space, S = {E1 U E2 U E3, .....U En}

Let us consider an event A within the sample space S:

A = A ∩ S ( A is a subset of S)

Therefore,

A = A ∩ {E1 U E2 U E3, .....U En}

Or, A = {A ∩ E1} U {A ∩ E2} U {A ∩ E3}, .....U {A ∩ En}

Now, let us apply probability to both sides of the equation:

P(A) = P(A ∩ E1) U P(A ∩ E2) U P(A ∩ E3), .....U P(A ∩ En)

P(A) = P(A ∩ E1) + P(A ∩ E2) + P(A ∩ E3), .....U P(A ∩ En)

Therefore, the formula for the law of total probability,

P(A) = P(E1)P(A/E1) + P(E2)P(A/E2) + ......P(En)P(A/En)

In simpler terms, this equation represents the probability of event A as the sum of probabilities of A happening given each of the mutually exclusive events E1, E2, E3, ..., En, weighted by the probabilities of those events occurring.

Moreover, it is a fundamental concept in probability theory involving conditional probabilities. It is closely linked with Bayes Theorem, which is widely used in various fields. While calculators are available to compute probabilities using this law, its proof involves a thorough understanding of conditional probabilities and their application.

Examples

Let us use a few examples to understand the topic.

Example #1

Consider Student A at Ludon University preparing for the engineering final exam. This scenario involves three study habits: regular studying, last-minute cramming, or not studying at all. Relevant data includes pass rates:

Students regularly studying have a likelihood of passing = 60%

Students opting for last-minute cramming possess a chance of passing = 30%

Students abstaining from studying have a probability of passing = 10%

Additionally, the following is the information regarding the distribution of students across these study habits:

Students following regular study routine = 40%

Students resorting last-minute cramming = 30%

Students refraining study = 30%

The Law of Total Probability is applied to ascertain the probability of Student A successfully passing the engineering exam:

P(A) = P(A|Regular Study) * P(Regular Study) + P(A|Last-Minute Cram) * P(Last-Minute Cram) + P(A|No Study) * P(No Study)

By substituting the provided values, one determines:

P(A) = (0.6 * 0.4) + (0.3 * 0.3) + (0.1 * 0.3) = 0.24 + 0.09 + 0.03 = 0.36

Consequently, Student A possesses a 36% likelihood of successfully passing the engineering final exam.

Example #2

The law of total probability is employed in the case of SARS-CoV-2 in England to quantify and understand the intensity of hospital transmission cases. This research studies the higher transmission risks associated with hospitalized individuals who are more prone to catching viral infections because of interactions. The probability theory takes into account several factors, including identifiable hospital-acquired cases, nature and distribution of infections evident by PCR tests and testing policies to estimate the cumulative number of infections spread through hospitals.

Applications

The law of total probability is a foundational concept in probability theory that computes the probability of an event by considering all possible outcomes and their associated probabilities. It finds applications in diverse fields, as listed below:

Bayesian Inference: It is necessary for calculating posterior probabilities based on fresh evidence.
Decision Analysis: It puts to use the law of total probability to determine the anticipated value of alternative decisions in the presence of uncertainty.
Risk Assessment: It helps to assess total risk by considering numerous potential outcomes.
Reliability Engineering: The technique helps evaluate the robustness of complicated systems while taking into account various failures of probability.
Queuing Theory: It aids in including arrival rates and service durations into performance measurements like average wait time and line length.

Frequently Asked Questions (FAQs)

1. When to use the law of total probability?

A key idea in probability theory is the Law of Total Probability, which enables one to determine the likelihood of an occurrence by considering all potential events and their corresponding probabilities. It is employed when several mutually exclusive occurrences together span the full sample area.

2. What is the point of the law of total probability?

The major goal of using the Law of Total Probability is to deal with circumstances in which one possesses only partial information regarding an event but is aware of its conditional probability under many scenarios. We may fully comprehend the entire likelihood by taking into account all conceivable outcomes and their respective probabilities.

3. Where is the law of total probability?

It may be found in several disciplines that deal with uncertainty and probability, including decision theory, statistics, and mathematics. It is a fundamental idea that is applied in several fields, such as risk evaluation, insurance pricing, machine learning algorithms, and Bayesian inference.