Law of Large Numbers

Published on :

21 Aug, 2024

Blog Author :

Edited by :

Reviewed by :

The Law of large numbers in mathematics states that the sample mean acquired from a set of values has a higher chance of being closer to the actual mean when the sample set of values is larger. The more the number of trials, the greater the chance of arriving at an accurate value.

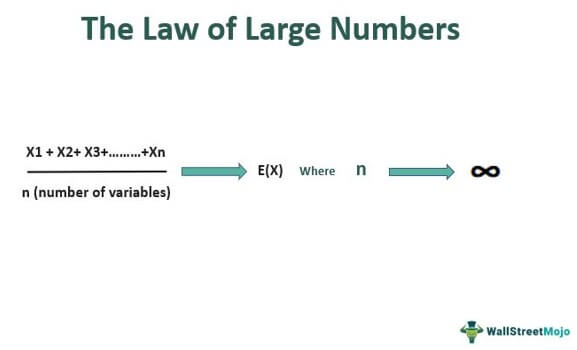
Therefore, one can reveal true potential and accurate characteristics if they take a larger group of samples. In other words, each additional trail will increase the chances of arriving at the exact expected value. Accordingly, the Law of large numbers has a wide range of applications in real life.

What is the Law of Large Numbers?

The Law of large numbers states that the larger the sample, the more likely the sample mean will be closer to the distribution mean.
This is especially useful for approximating huge calculations and enhancing the chances of accuracy in a given setting. Obtaining a figure closer to the actual mean or average improves the data's reliability and can assist one in making important decisions.
A person can apply it to a range of businesses, including estimating the premium to be set in the insurance industry, forecasting growth forecasts in a corporation, and determining demographic characteristics in statistics, among others.

Law of Large Numbers Explained

The Law of large numbers or "the Golden Theorem" or "Bernoulli's theorem" was curated by Jacob Bernoulli, a Swiss mathematician. The theorem later became known as "The Law of large numbers." It states that an unknown proportion can reach a degree of accuracy through an appropriate number of trials. The theorem is usually used to optimize sample sizes and approximate calculations that are complicated. It is of two types- the strong Law of large numbers and the weak Law of large numbers.

The Weak Law of large numbers reveals that if there is a set of independent and identically distributed random variables, the sample mean will converge in probability towards the actual mean. If the sample means must meet the distribution mean, evaluation can use a large sample set of values. But the strong Law states that the sample mean and distribution mean will converge closer to the actual value. The Weak Law and the strong Law of large numbers are quite different from each other and their function differs.

The Law, however, differs from the "gamblers fallacy", which is a thought process where people predict a certain set of events happening based on the previous set of circumstances. Say, in a situation of 50 events of flipping a coin, there have already been 20 heads. The person will expect the rest of the events to result in tails as there had been an upstart of heads way ahead. The Law of large numbers does not support the theory of events suddenly developing bias towards a particular event.

Law of Large Numbers in Statistics

The Law of large numbers can be particularly useful in the case of statistics. For example, suppose we need to determine a village's average age.

Let's say that particular village has around 1000 people. If we take the ages of five people, i.e., 20,30,40,50, and 60, the sum of all the numbers is 200. Taking the average, 200/5 ( number of total values taken), gives us the mean value of 40. Therefore, the average age of that group is 40. This small sample of 5 people is far too small to represent a sample of 1000 people. When there is a large sample of ages, the values vary. Let's say the average age of 10 people now is 50. There is an obvious shift of value from the previous value of 40. This higher value shift will have greater chances of being near the value of the actual average age of the village's population. Statistics uses similar applications of the Law to find the population, life expectancy, and literacy ratios of a nation.

Law of Large Numbers Examples

Example #1

Suppose there is a competition for flipping coins between two persons, A and B. The person who gets the most number of tails is the winner. However, they are yet to determine the number of times they are allowed to flip a coin. Initially, in the event of flipping a coin, the probability is 1/2. i.e., for each flip, the chance of landing a tail is 0.5. Suppose they flip the coin 20-30 times and there were tails only seven times. Flipping it ten more times can move the score to 9 tails. The more one flips the coin, the greater the chances of arriving at the proportion of the decided ratio, i.e., 0.5.

Example #2

Suppose Sam is an investor and there are three famous companies- "ABC," "CDE," and "EFG." He decides to invest in a company that has the potential to increase its market value by 50% in a short period. Say ABC is valued at $40 million, CDE has $80 million, and EFG has only $4 million. So looking at them, we know 50% for ABC will be $20 Million extra; for CDE, it will be $40 Million. And for EFG, it will be a $2 Million market value increase. So looking at it, EFG needs only a small amount to grow, and Sam can choose EFG according to the growth prediction he made.

Law of Large Numbers in Insurance

The Law of large numbers helps insurance companies reduce the risk of loss by pooling information on a large number of people. Let's take the example of a car insurance company ABC Ltd. The company collects data from people of all ages to gather information on their age and the number of accidents caused. This will help determine what premium to charge for a particular part in that age group. For example, if the accidents are caused mostly by people aged 25, then people belonging to that category will be charged higher.

Charging higher premiums for that particular age group can help recover losses due to accidents caused by them. These companies arrive at such a conclusion after following many people's details, like a small sample of people may not contain the required age groups and reveal any important information. The insurance field uses similar applications in house insurance, health insurance, and other vehicle insurances.

Frequently Asked Questions

How does one use the Law of large numbers?

This particular technique can be used in various industries, such as determining the premium to be set in the insurance industry, predicting growth forecasts in a corporation, and so on.

What is the weak and strong Law of large numbers?

The Weak Law of large numbers definition states that if a set of independent and identically distributed random variables exists, the sample mean will converge towards the actual mean. The sample mean can be brought closer to the distribution mean by using a large sample set of values. The strong Law of large numbers definition, on the other hand, states that the sample mean and distribution mean will converge closer to the true value.

Why is the Law of large numbers useful?

The Law is particularly effective for approximating large calculations and increasing the likelihood of accuracy in a situation. Getting a figure closer to the real mean or average increases the data's reliability and can help one make key decisions.