Law of Diminishing Returns

The law of diminishing returns states that an additional amount of a single factor of production will result in a decreasing marginal output of production. The law assumes other factors to be constant. It means that if X produces Y, there will be a point when adding more quantities of X will not help in a marginal increase in quantities of Y.

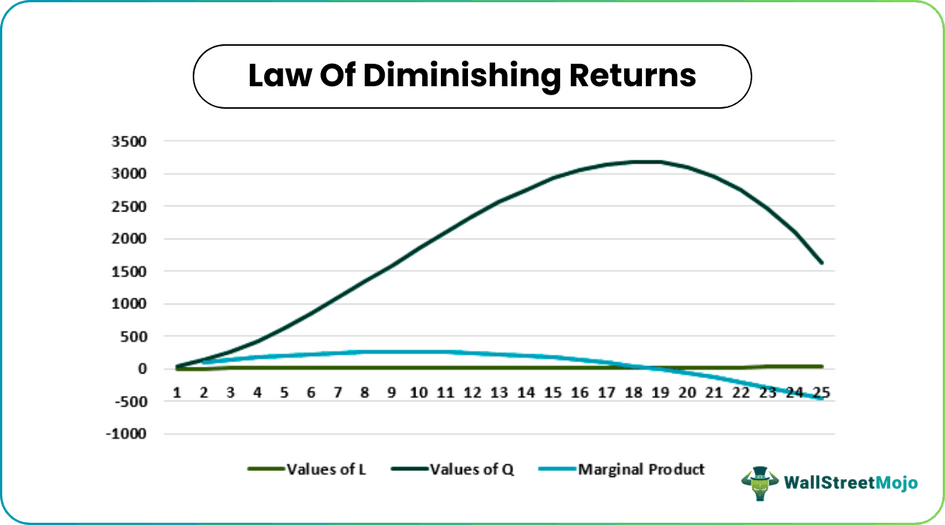
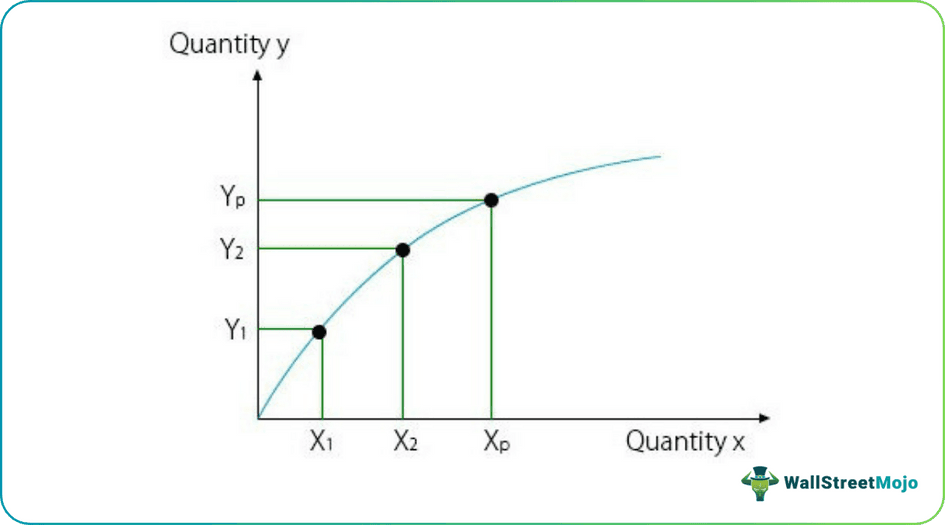
In the below graph of the law of diminishing returns, as factor X rises from 1 unit to 2 units, the number of Y increases. But as X quantities rise further to P, production assumes a decreasing rate till Yp. This describes the law above. Another noticeable aspect is that there comes a point when a further increase in units of X will only reduce the production of Y. Thus, not only does increasing input affect marginal product but also the total product.  This law is mostly applicable in a production setting.

There are three components from the definition of the law of diminishing returns.

1. The Factor of Production – Any input that generates a desired quantity of output. Concerning the law of diminishing returns, only one factor at a time is considered.
2. Marginal Product – With every additional input, the increase in the total product is referred to as the marginal product. In the graph above, Y₂-Y₁ is the marginal product.
3. Total Product – When an input is applied through a process, the total product is the result or outcome as an aggregate measure.

• The law is used mostly by considering a short-run production scenario. That is because the principle lies in keeping all other factors of production constant, except the one used to correlate with output. It is not possible in a long-run view of production.
• The input and the process(es) should be held independent of technological aspects as technology can play its part in improving production efficiencies.

Below are examples of the law of diminishing returns.

Example #1

Suppose that a factory produces a certain good given by the following equation:

Q = -L³ + 27L² + 15L

Where,

Q is the quantity of production

L is the input in terms of labor

Describe if the law of diminishing returns applies. If yes, how?

Solution:

To check the applicability of this law, we will quantify units of production by assuming different values of labor input.

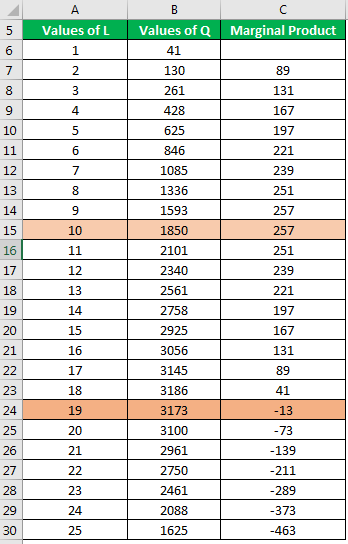
We have plotted the values of Q and L on a graph for analysis. The Y-axis represents the product (total and marginal). The X-axis represents units of labor.

In the above law of  diminishing return graph, two points are critical to the law:

• Point A - the limiting marginal product, and
• Point B - the limiting total product.

The following points are worth noting:

We can divide this production graph into two stages concerning the marginal output.

1. As labor input increases, the marginal product also increases before the number of workers, L = 9. It is the stage of growing returns.
2. The marginal product produced by the 11th unit of labor is less than the 10th. It begins the stage of diminishing returns.

The total product, i.e., Q's quantity, does not decrease before the 20th worker is employed. The marginal product enters the stage of negative returns from here.

The factory can employ 9 workers to keep the marginal product at a rising rate. However, it can add as many as 19 workers before noting a fall in the total product.

Example #2

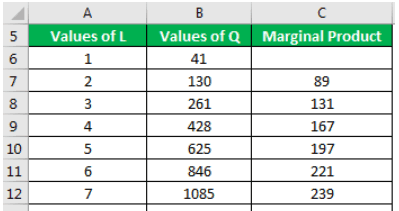
A farmer owns a small wheat field. He starts cultivating his land with one laborer. He gradually increases it to six laborers only to find that his wheat output has not proportionately increased. Help the farmer out in analyzing the optimal workforce required.

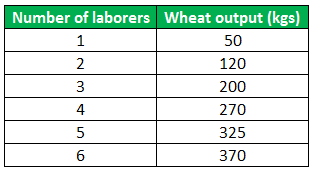
Solution:

By simply looking at the wheat output against the labor used, we can say that the marginal output decreases with each additional labor deployed. Therefore, if we deduce the marginal product and present it to the farmer, it will look like this:

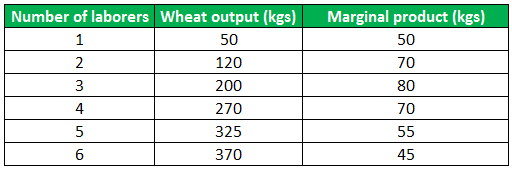
It shows that the marginal product increases before the services of the 4^th laborer are taken. After that, the marginal product decreases.

Hence, the farmer should optimize his wheat output with 3 laborers on his field.

On the other hand, he can maximize his total product by continuing to increase laborers. But this comes at the cost of reduced marginal output.

These two examples are from a good stage from where we can look at the advantages and limitations of the "law of diminishing returns."

• The law of diminishing returns helps management maximize labor (as in examples 1 and 2 above) and other factors of production to an optimum level.
• This theory also helps increase production efficiency by minimizing costs, as evident from the wheat farmer's case.

• Although useful in production activities, we cannot apply this law in all forms of production. The constraint comes when the factors of production are less natural. Hence, a universal application is difficult. Mostly this law finds its application in agricultural scenarios.
• The law assumes that all units of a single factor of production must be identical. It is, however, not practical usually and becomes a hurdle in an application. In our above examples, labor becomes the specific input, and other factors are held constant.

The law of diminishing returns is a useful concept in production theory. The law can be categorized into increasing returns, diminishing returns, and negative returns. The production industry, particularly the agriculture sector, finds the immense application of this law. Producers question where to operate on the graph of the marginal product as the first stage describes underutilized capacity, and the third stage is about overutilized inputs. Hence, to arrive at the optimum capacity is the rationale behind this law.