Laspeyres Index

Laspeyres Index is a methodology to calculate the consumer price index by measuring the change in the price of the basket of goods in the present year to the base year. It was invented by Etienne Laspeyres, an economist from Germany, to analyze the changes in the prices compared to the base year period.

• The index generally uses a base year of 100 to analyze the index. An index greater than 100 implies a rise in prices, and an index less than 100 means a fall in prices.
• Year 0 is termed as the base year, while the calculating year will be termed as an observation year period.
• Economists use it more to analyze the country's economic growth, considering the inflation in goods and services.

1. The Laspeyres index is a method for calculating the consumer price index that compares the current year's price of the basket of items to the base year. 
2. German economist Etienne Laspeyres developed it to examine price fluctuations relative to the base year era.
3. Since base year numbers were used and the current quantities were disregarded, it provides a realistic representation and value of the commodities.
4. The government will implement new market-clearing rules in response to a significant change in the Laspeyres pricing index, decreasing the effect of price increases on the general populace.

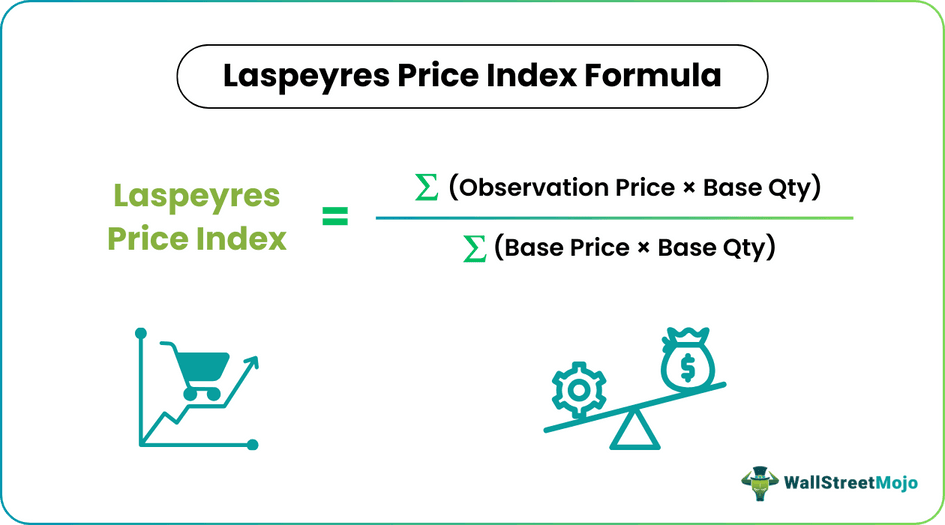
Laspeyres Index Formula= ∑ ( Observation Price * Base Qty) / ∑ ( Base Price * Base Qty)

Where,

• Observation price refers to the price at the current levels for which the index needs to be calculated.
• Observation quantity refers to the quantity at the current levels for which the index must be calculated.
• Base price refers to the price at year 0, known as the base year for calculating the index.

Let's take an example for a better understanding of this index.

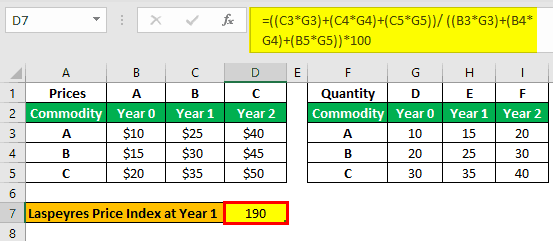
Let us take the below-mentioned example to understand the calculation of the Laspeyres price index for commodities A, B & C.

Solution :

In the above example, to calculate the Laspeyres price index, the quantities for the future years are not required; hence the same has not been plotted in the table. However, below mentioned are the steps to calculate the Laspeyres price index.

Laspeyres price index at year 0 = 100. Since both the numerator and denominator here will be the same, the base year result would be 100, which shall be used in future years to compare the performance of the goods and services and draft a suitable plan of action to control the same if there is any excessive price rise or decline which would affect the consumers directly and in turn the economy.

This index will show a relative and absolute valuation without considering the future changes in the economy and the government policies, which keep on changing every year to benefit the common public at large.

Calculation of Laspeyres Price Index at Year 1 will be –

Laspeyres Price Index formula for year 1 = {(25*10)+(30*20)+(35*30)} / {(10*10)+(15*20)+(20*30)}

Index at year 1 = 190

Calculation of Laspeyres Price Index at Year 2 will be –

Laspeyres Price Index formula for year 2 = {(40*10)+(45*20)+(50*30)} / {(10*10)+(15*20)+(20*30)}

Index at year 2 = 280

Hence we can observe the inflation impact in the prices since the prices increased from 100 to 190 in year one and finally up to 280 in year two, the price of commodities have climbed up.

It is one of the most important tools to observe the inflation in the basket of goods and services by comparing the current price levels with the base year quantities.

Below mentioned are some of the major advantages of the Laspeyres index ratio:

• It is very easy to calculate in an excel sheet.
• It focuses only on base year quantities and current level prices; hence, there is no need to calculate the quantities for future years.
• It gives a fair picture and value of the commodities since base year quantities have been used, thus ignoring the current level quantities.
• It is a good parameter to frame future policies that will control inflation.

• It does not take into account the current level of quantities.
• It ignores the growing economy.
• Since there can be a change in the production level in the future years, ignoring this fact will not be correct in the model.
• It completely ignores the new entrants in the market.
• It does not consider the change in quality and substitute goods that can have a major impact on the prices.
• In the case of substitute goods, the old ones that become obsolete may push the price up to the production levels. Hence ignoring the future quantities will not show a correct index figure and will have a direct impact on the government policies ahead.

• More mathematical, less practical.
• It is not used commonly among economists since the Pastiche index gives a better picture.
• Prices tend to rise every year, keeping in mind the consumption patterns and rising living standards.
• Deciding on the base year is a major challenge.

A significant change in the Laspeyres price index will trigger the government to control the growing inflation by implementing new policies that will clear the market, thereby reducing the price rise pressure on the common public.

It is one of the key ratios to determine the speed of inflation for goods and services. However, since this index is different from the Paasche price index, which uses current level quantities in its formula, while the Laspeyres price index uses base year quantities, both cannot be compared and will give an altogether different picture reflecting on the rise or fall in the prices.

Economists have widely used this index to make the country's financial and economic decisions and drive the consumer market without passing on the pressure of price rise to the common public.

This has been a guide to the Laspeyres Index and its definition. Here we discuss the formula to calculate the Laspeyres Price index along with an example and advantages and disadvantages. You can learn more about accounting from the following articles –

• Examples of Heckscher Ohlin Model
• Veblen Goods
• Stackelberg Model Meaning
• Cost-Push Inflation Causes