What is the Joint Probability?
Joint Probability is the possibility of occurring one or more independent events at the same time, denoted as P (A∩B) or P (A and B) and is calculated by multiplying the probability of both the outcomes = P (A)*P (B)
Step 1- Find the Probability of Two events separately
Step 2 – To calculate joint probability, both the probabilities must be multiplied.
You are free to use this image on your website, templates etc, Please provide us with an attribution linkHow to Provide Attribution?Article Link to be Hyperlinked
For eg:
Source: Joint Probability Formula (wallstreetmojo.com)
Examples of Joint Probability Formula (with Excel Template)
Example #1
Let’s consider a simple example. A bag contains 10 blue balls and 10 red balls if we choose 1 red and 1 blue from the bag on a single take. What will be the joint probability of choosing 1 blue and 1 red?
Solution –
- Possible outcomes = (red, blue),(blue, red),(red, red), (blue, blue)=4
- Favorable outcomes = (red, blue) or (blue, red) = 1
Use below given data for calculation
| Particulars | Value |
|---|---|
| Number of Red Balls | 10 |
| Number of Blue Balls | 10 |
| Probability of Choosing 1 Red and 1 Blue | 1 |
| Possible Outcomes | 4 |
Probability of choosing red ball
- P (a) = 1/4
- = 0.25
Probability of choosing a blue ball
- P (b) = 1/4
- = 0.25
- =0.25*0.25
Example #2
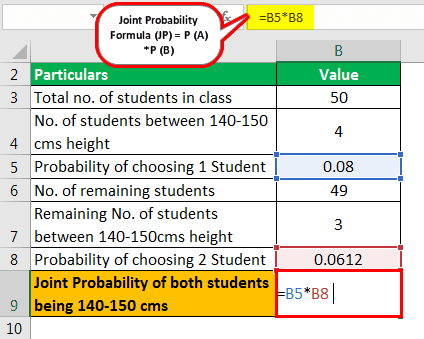
You have students strength of 50 in a class, and 4 students are between 140-150cms in height. If you randomly select one student and without replacing the first selected person, you are selecting the second person what is a probability of both being between 140-150cms.
Solution
Use below given data for calculation
| Particulars | Value |
|---|---|
| Total no of students in class | 50 |
| No of students between 140-150 cms height | 4 |
First, need to find the probability of choosing 1 student in the first draw
- P(a) =50*4
- =0.08
Next, we need to find the second person between 140-150cms without replacing the selected. As we already selected 1 from 4 the balance will be 3 students.
Probability of choosing 2 student
- P(b) =50*4
- =0.08
- =0.08*0.0612
Therefore, the Joint Probability of both students being 140-150cms will be –
Example #3
There was a survey with Full-timers and Part-timers in a college to find how they are choosing a course. There were two options, either by the quality of a college or by the cost, of course. Let’s find the joint probability if both full-timers and part-timers choose cost as the deciding factor.
Solution
Use below given data for calculation
| Particulars | Cost | Quality | Total |
|---|---|---|---|
| Fulltime | 30 | 70 | 100 |
| Part-time | 60 | 50 | 110 |
| Total | 90 | 120 | 210 |
Probability of full-timers in college
- =30/210
- Full-timers = 0.143
Probability of part-timers in college
- =60/210
- Part-timers = 0.286
Joint Probability of full-timers and part-timers is calculated as follows,
- =0.143*0.286
Difference Between Joint, Marginal, and Conditional Probability
- JOINT PROBABILITY – It is the possibility of occurring one or more independent eventsIndependent EventsIndependent event refers to the set of two events in which the occurrence of one of the events doesn’t impact the occurrence of another event of the set.read more at the same time. For instance, if an event Y appears and the same time event X appears, it is called a joint probability.
- CONDITIONAL PROBABILITY – if one event has to occur, then the other event is already known, or true, then it is called a Conditional Probability. e.g., if event y has to be, then the event X must be true.
Conditional probability occurs when there is a conditional that the event already exists or the event already given has to be true. It can also be said as one event is dependent on the occurrence or existence of another event.
- MARGINAL PROBABILITY – It is simply referred to as the probability of occurrence of a single event. It does not depend on another probability of occurring like conditional probabilityConditional ProbabilityConditional probability refers to the chances of a particular event occurring, provided another event has previously occurred. It is widely applicable in many areas, including business risk management, insurance, personal life, calculus, politics, etc., helping individuals and entities identify possible outcomes and make practical decisions accordingly. read more.
Both conditional and joint probabilities deal with two events, but their occurrence makes it different. In conditional, it has an underlying condition, whereas in joint, it just occurs at the same time.
Let’s consider an example if the price of crude oil increases, then there will be an increase in the price of petrol as well as in gold. If both gold and petrol prices increase at the same time, it can be said as joint probability, but with joint probability, we can’t measure how much one influences the other, there comes conditional probability it can be used to measure how much one event influence the other.
Relevance and Use
When two are more events occurring at the same time, the joint probability is used, mostly used by statisticians to indicate the likelihood of two or more events occurring same time, but it does not how they influence each other.
We can just use to know the value of both events occurring together, but will not show how far one event will influence the other.
Recommended Articles
This has been a guide to Joint Probability and its definition. Here we discuss the formula for calculation of joint probability along with practical examples and a downloadable excel template. You can learn more from the following articles –
- 16 Courses
- 15+ Projects
- 90+ Hours
- Full Lifetime Access
- Certificate of Completion
58.6K subscribers