ITO's Lemma

Publication Date :

29 Jan, 2025

Blog Author :

Edited by :

Reviewed by :

Table Of Contents

What Is ITO's Lemma?

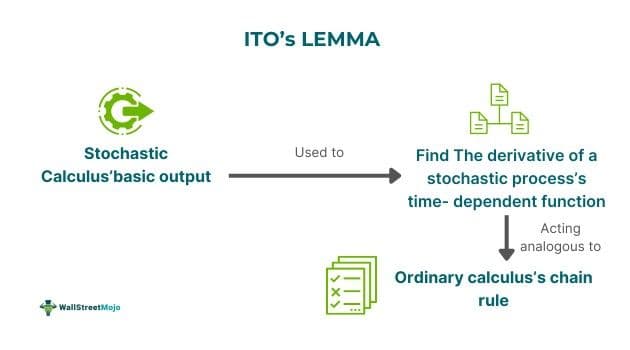
ITO's lemma refers to the basic output in stochastic calculus used to find the derivative of a stochastic process's time-dependent function, acting analogously to ordinary calculus's chain rule. It acts as quantitative finance's cornerstone and is essential to calculating the Black-Scholes equation related to options or price contingent claims.

You are free to use this image on your website, templates, etc.. Please provide us with an attribution link.

It facilitates log-normal-fashioned modeling of asset price distribution using the extension of simple calculus. To understand its application in the finance field, one needs to know ITO's Lemma derivation and geometric Brownian motion.

Key Takeaways

ITO’s lemma is a fundamental outcome in stochastic calculus used to determine the derivative of the time-dependent function of a stochastic process that functions similarly to the chain rule in ordinary calculus.
It is the foundation of quantitative finance, which is necessary to solve the Black-Scholes equation for claims involving price-dependent contracts or options.
Its commonly existing formula is a stochastic differential equation as shown below: dF = FxdX + Ftdt + .5Fxxσ2dt dF = [Fτ + Fxμ + .5Fxxσ2] dt + FxσdWt.
Understanding Brownian motions, deriving valuation formulae, calculating derivative prices, determining time-dependent functions, and calculating infinitesimal generators is essential.

ITO's Lemma In Quantitative Finance Explained

ITO's lemma captures both deterministic and random aspects of change by breaking down the variation of a function concerning a stochastic process into numerous parts. It comprises widening the function utilizing the Taylor series and conserving terms that represent the increase in stochastic process and time. Moreover, it is conventionally modeled as a Brownian motion and Weiner process.

It has many implications in quantitative finance because it offers the underpinning of mathematics related to derivative pricing models involving the renewed Black-Scholes equation. Understanding the risk management and pricing of derivatives has been vital, as they permit stochastic processes.

It has become a vital tool in the financial industry for modeling asset prices' random motion and solving the SDEs related to different financial instruments. Moreover, it covers different stochastic process types like poison jump and drift-diffusion processes, forming a versatile technique in the sector.

Its impact on the financial world has become transformative, creating the base of modern financial mathematics. It has also led to the growth of complicated models concerning risk management and option pricing. It has influenced the way in which financial markets function. And it has become the cornerstone of analyzing uncertain financial instruments quantitatively.

Formula

Different rules of computing integral or derivative can be extended to lTO's stochastic calculus to calculate the Ito lemma. However, deriving its formula is too difficult and technical, requiring proof of ITO's lemma. Therefore, only a heuristic approach is enough for deriving its formula.

Therefore, its formula is

F(X(t), t) = F(X(0), 0) + t 0 dτ + t 0 FxσdWt.

However, its formula commonly exists as a stochastic differential equation, as shown below:

dF = FxdX + Ftdt + .5Fxxσ2dt dF = dt + FxσdWt

Examples

Let us use a few examples to understand the topic.

Example #1

Let us assume that Dana has a lemonade shop in a bustling corner of Old York City. Her shop receives an unpredictable amount of customer flow. She wants to understand the net profit from her shop. She utilizes ITO's lemma for the purpose by assuming that her:

Profit relies on the number of lemonade customers, just like mathematical functions and the cost of lemons, which acts as a variable.
She notes and discloses these changes, including the arrival of random customers that affect her overall profit.

Now, by using ITO's lemma, she can break down her profits from the lemonade shop into:

The random part, which is the impact of customer flow
The predictable part is average price changes.

Thus, she has been able to set the price of her lemonades by considering the two factors and obtain maximum profits.

Example #2

An online article published in 2014 discusses assessing market fluctuation using ITO’s lemma along with Brownian motion centering on the Colombo stock exchange (CSE). The article stresses the significance of data forecasting concerning economic time series in guiding financial decisions during volatile and uncertain markets. The research tried to develop forecasting relying on geometric Brownian motion to determine the share price indices related to short-term investments in CSE.

Further, the study contrasts the new model against the traditional Autoregressive Integrated Moving Average (ARIMA) approach, finding that the proposed model is more significant to investors in making profitable investment decisions. Hence, it showed that stochastic processes and lTO's lemma can be used to resolve real-world financial problems, especially in relation to managing and forecasting financial market volatility.

Importance

Its importance is as follows:

Has been a vital tool for deriving valuation formulae.
Describes the manner in which functions of Brownian motions act.
Helps calculate stochastic process model’s infinitesimal generators in finance.
Determines time-dependent function related to a stochastic process.
Vital in deriving option pricing's Black-Scholes equation.
Facilitates modeling asset price distribution within a log-normal manner by extending the rule of chain to random variables.
The price of derivatives can be calculated by deriving the stochastic differential equation (SDE).