Interest Rate Parity
Last Updated :
21 Aug, 2024
Blog Author :
Edited by :
Ashish Kumar Srivastav
Reviewed by :
Dheeraj Vaidya, CFA, FRM
Table Of Contents
What Is Interest Rate Parity?
Interest Rate Parity is a concept that links the forex market rate and a country's interest rates and states that if the currencies are in equilibrium, one cannot make use of the opportunity to make profits just by exchanging money.
The underlying concept is that investment returns in various currencies should be independent of the country's interest rates. Hence, there will be no arbitrage opportunity in the foreign exchange markets – investors cannot seek to profit from the difference between the interest rates using foreign exchange as an asset or a way to invest.
Table of contents
- What Is Interest Rate Parity?
- Interest Rate Parity is a concept that ties the forex market rate to a country's interest rates and says that if the currencies are in equilibrium, one cannot exploit the potential to produce benefits merely by exchanging money.
- The basic premise is that interest rates in a country should not impact investment returns in other currencies. Arbitrage in the foreign currency markets is impossible since investors cannot utilize foreign currencies as an asset or a means of investment.
- Interest rate parity can be uncovered or covered. Uncovered relies on expected spot rates, while covered involves predetermined contracts with fixed forward rates.
Interest Rate Parity Explained
The interest rate parity theory is the concept which establishes a relationship between the exchange rates and the interest rates, and the expected rate of return between two countries. According to the theory, the difference between the exchange rates between two countries equals the difference between the spot exchange and the forward exchange rate.
Put – a person who invests in a domestic country and then converts into other currencies or another who converts into other currencies and invests in the international market will yield the same return, considering all other factors constant.
They are of two types – uncovered and covered interest rate parity. The former interest rate parity condition exists when there are no covenants about the forward interest rate, and the parity is dependent only on the expected spot rate. In other words, the investor can borrow in one currency, change it to another currency and invest it in the prevailing interest rate, and then convert it back to the original currency; they get no chance to go for risk-free gains. In the latter's case, a pre-decided contract is locked in for the forward interest rate. In layman's terms, we forecast the uncovered rates while we lock in the covered rates today. Here the investor does not cover the exchange rate risk with forward contracts.
This topic opens a lot more avenues to explore. This Advanced Derivatives course throws insight into the deeper aspects of Interest rate parity.
Formula
Numerically, interest rate parity theory can be put as –
Forward Exchange Rate (Fo) = Spot Exchange Rate (So) X (1 + Interest rate A)^n / (1 + Interest rate B)^n
It can also be put as –
Forward Exchange Rate (Fo) / Spot Exchange Rate (So) = X (1 + Interest rate A)^n / (1 + Interest rate B)^n
The interest rate parity equation explains that the forward exchange rate (Fo) should equal the spot exchange rate (So) multiplied by the interest rate of country A (home country) divided by the interest rate of country B (foreign country). The gap between Fo and So is termed a swap. A positive difference is known as a forward premium; conversely, a negative difference is called a forward discount.
In cases where Interest Rate Parity stands good, it is impossible to create an interest rate parity arbitrage/ profit opportunity by borrowing currency A, converting it into currency B, and returning to the home currency in the future.
Examples
Let us understand the concept of interest rate parity condition with the help of some suitable examples given below:
Example #1
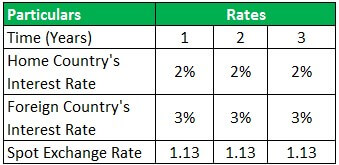
Let us assume a spot rate of 1.13 USD/ EUR, a USD interest rate of 2%, and a EUR interest rate of 3%. What will be the Forward Exchange Rate after a year?
Solution
Use the below-given data for the calculation of the forward exchange rate –
Calculation of forwarding Exchange Rate can be done as follows –
- = 1.13*(1+2%)^1/(1+3%)^1
Forward Exchange Rate will be -
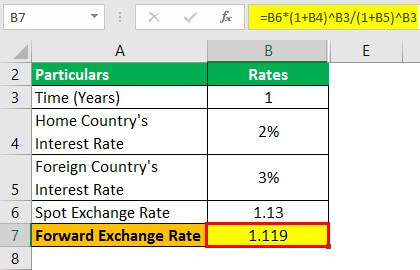
- Forward Exchange Rate = 1.119
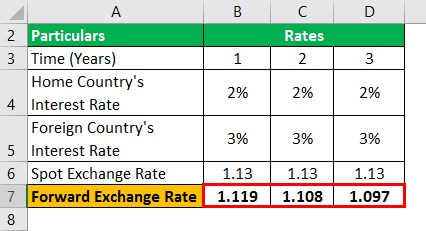
Similarly, we can calculate forward exchange rate for year 2 and year 3
Example #2
Suppose the USD to CAD spot exchange rate is 1.25, and the one-year forward exchange rate is 1.238. Now, the interest rate for USD is 4%, while it is only 3% for CAD. If IRP were to hold, it would mean – 1.2380 / 1.2500 should be equal to 1.03 / 1.04, which turns out to be approximately 0.99 in both cases, which confirms the validity of the Interest Rate Parity.
Example #3
Taking a step further, let us assume person A is investing USD 1,000 in a year. There are two scenarios – one, wherein we can invest in EUR and convert it into USD at the end of year one or two, where we can convert into USD now and invest in USD. Suppose So = 0.75 EUR = 1 USD, interest rate in EUR is 3% and USD is 5%.
Scenario 1
If the interest rate in EUR is 3%, A can invest USD 1000 or EUR 750 (taking FX rate) at 3%, giving a net return of USD 772.50.
Scenario 2
Otherwise, A can invest in USD 1000 and then convert the return into a net return. Fo = 0.75 (So) X 1.03 (home currency)/1.05 (foreign currency) = 0.736
Now, USD 1000 at 5% yields USD 1050, which can be converted into EUR using 0.736 and not 0.75 as the conversion rate.
Therefore, USD 1050 = USD 1050 X 0.736 giving a net return of approximately USD 772.50.
Assumptions
The theory follows certain assumptions as given below:
- It assumes that the there is efficiency in the financial markets and they are also free of any restriction or transaction cost which hampers the movement of capital
- It also assumes that there is no opportunity to make risk-free profits. Capital will flow till the chance to gain becomes nil, thus making the interest rate and exchange rate equal.
- According to the theory, capital can move freely across countries.
- It assumes that the risk of investment in different currencies is similar. There is no extra risk for investment in international currency as copared to domestic currency.
- As per the theory, the market participants are rational and unbiased.
Advantages
The concept has some important advantages as follows:
- Interest rate parity is essential because if the relationship does not hold well, there is an opportunity to make an unlimited profit by borrowing and investing in different currencies at different points, termed interest rate parity arbitrage.
- Suppose the forward exchange rate exceeds the calculated Interest Rate Parity rate. In that case, a person can borrow money, convert it using a spot exchange rate and invest in the foreign market at interest rates. At maturity, it can be converted back to a home currency with a fixed profit since the locked price is greater than the calculated price.
- Interest rate parity can also be used to determine the pattern/ estimate of the foreign exchange rate at future dates. For instance, if the interest rate of a home country is increasing, keeping the interest rate of a foreign country constant – we can speculate the home currency to appreciate over the foreign currency. The opposite holds if we see the interest rate of the home country decreasing.
Disadvantages
The disadvantages of the theory are given below:
- The interest rate parity equation is still criticized for the assumptions it comes up with. The model assumes that one can invest in any fund and currency available in the market, which is not practical and realistic. Also, when there is no scope to hedge the future/ forward contracts, the uncovered IRP stays null and void.
- Technically, anyone and everyone would have made money by borrowing funds and investing in different markets – which is not practical and does not hold in the real world.
Interest Rate Parity Vs Purchasing Power Parity
The two important economic concepts above establish a relation between prices, exchange rates, and interest rates. However, they focus on different aspects as given below:
- The former deals with the relation between the exchange rates and interest rates whereas the latter deals with the relation between the price levels and exchange rates.
- The former suggests that the difference between the interest rate between two currency should equal the change in the exchange rates, whereas the latter suggests that the exchange rate between the two currencies must adjust to be equal to the purchasing power of the two currencies.
- The former can be either covered or uncovered, but the latter can be either an absolute or relative purchasing power parity.
Thus, the above are some important differences between the two concepts. But it is important to understand that the financial markets in the actual world experience the influence of various factors which may not be a part of the above theories.
Frequently Asked Questions (FAQs)
What is covered interest rate parity?
A situation when the relationship between interest rates and the spot and future values of two nations is in equilibrium is known as covered interest rate parity.
Is interest rate parity a theory?
ccording to the interest rate parity (IRP) hypothesis, the difference in interest rates between two nations equals the difference between the forward and spot exchange rates.
What is interest rate parity also known as?
Interest rate parity (IRP) is when the rates of return on equivalent assets in two nations are identical. It is a hypothesis used to explain the value and changes in exchange rates. It is also known as the asset method of exchange rate setting.
Does interest rate parity always hold true?
Interest rate parity is a theoretical concept that sometimes holds perfectly in real-world situations due to various factors. Market dynamics, geopolitical events, and changes in investor sentiment can lead to deviations from the expected relationships outlined by the theory.
Recommended Articles
This has been a guide to what is Interest Rate Parity. We explain the formula along with examples, differences with purchasing power parity & advantages. You can learn more from the following articles –
support@wallstreetmojo.com