The differences between inferential and descriptive statistics are listed as follows:
Table Of Contents
Inferential Statistics Definition
Inferential statistics helps study a sample of data and make conclusions about its population. A sample is a smaller data set drawn from a larger data set called the population. If the sample does not represent the population, one cannot make accurate estimations related to the latter. The purpose of studying inferential statistics is to infer the behavior of a population.
Unlike inferential statistics, descriptive statistics simply describes a data set without helping in drawing inferences. In this context, inferential statistics is said to go beyond the descriptive statistics. It is particularly used when it is not possible to examine each data point of the population.
Key Takeaways
- Inferential statistics involves making inferences for the population from which a representative sample has been drawn. Inferences are drawn based on the analysis of the sample.
- The procedure includes choosing a sample, applying tools like regression analysis and hypothesis tests, and making judgments using logical reasoning.
- The results include the sampling error. This error occurs when the researcher does not choose a sample that represents the population. To prevent the sampling error, one must select a random sample before applying the tools of inferential statistics.
- Descriptive and inferential statistics are two branches of statistics. The former describes the data set while the latter helps in making conclusions.
Inferential Statistics Explained
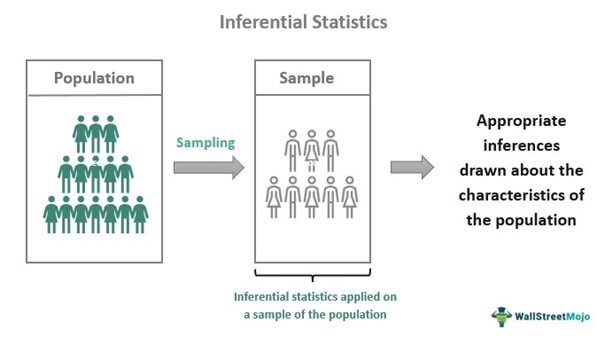
Inferential statistics allows researchers to make generalizations about a population by using a representative sample. However, since one cannot predict the behavior of a population accurately in almost all cases, the results are said to be based on uncertainty.
Further, the sampling error can be observed here. This error occurs if the sample drawn does not represent the entire population. To prevent this error, it is recommended to collect a random sample before applying inferential statistics.
Inferential statistics requires logical reasoning to arrive at the results. The procedure of reaching the outcomes is stated as follows:
- A sample is chosen from the population that needs to be studied. The chosen sample must reflect the nature and characteristics of the population.
- The tools of inferential statistics are applied to the sample to assess its behavior. These include the regression models and the hypothesis testing models. The former consists of linear regression, nominal regression, logistic regression, etc., while the latter consists of the z-test, t-test, f-test, analysis of variance (ANOVA), etc.
- Inferences are drawn from the sample chosen in the first step. The inferences are assumptions or estimations related to the entire population.
Types
Let us go through the types of tools used under inferential statistics.
#1 - Regression Analysis
It measures the change in one variable with respect to the other variable. Linear regression is popularly used in inferential statistics.
#2 - Hypothesis Testing Models
It requires creating the null and alternate hypothesis. Inferences are drawn by considering the critical value, test statistic, and confidence interval. A hypothesis test can be two-tailed, left-tailed, and right-tailed. The hypothesis testing models consist of the following tools:
a) Z-test
Z-test is used when the sample size is greater than or equal to 30 and the data set follows a normal distribution. The population variance is known to the researcher. The formulas are given as follows:
Null hypothesis: H0 : μ=μ0
Alternate hypothesis: H1: μ>μ0
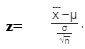
where,
- x̄ = sample mean
- μ = population mean
- σ = standard deviation of the population
- n = sample size
b) T-test
T-test is used when the sample size is less than 30 and the data set follows a t-distribution. The population variance is not known to the researcher. The formulas are given as follows:
Null Hypothesis: H0: μ=μ0
Alternate Hypothesis: H1: μ>μ0
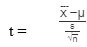
The representations x̄, μ, and n are the same as stated for the z-test. The letter “s” represents the standard deviation of the sample.
c) F-test
F-test checks whether a difference between the variances of two samples or populations exists or not. The formulas are given as follows:

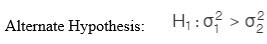
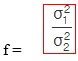
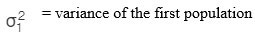
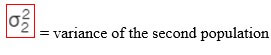
d) Confidence interval
It suggests the range within which the estimate will fall if the test is conducted on the population. When the confidence interval is high, one can state confidently that the sample results reflect the behavior of the population.
Example
Let us consider an example of inferential statistics.
Mr. A wants to open a coffee shop in New York, USA. To design the appropriate menu, a survey is conducted on 300 residents with the aim of understanding their tastes and preferences. The survey includes people of different age groups, gender, and income class. After applying the tools of inferential statistics, the results are stated as follows:
- 70% of women like the caramel macchiato.
- 50% of the total residents like café mocha.
- Almost 100% of the adults like Americano coffee.
- 25% of teenagers like café latte.
With these outcomes, Mr. A is confident that including all the above varieties of coffee will bring diverse customers to his shop. Moreover, Mr. A also wants to add new, innovative flavors to give a rich drinking experience to his customers.
Inferential Statistics vs Descriptive Statistics
| Differentiators | Inferential Statistics | Descriptive Statistics |
|---|---|---|
| 1. Definition | It helps make inferences about the population from which a representative sample has been drawn. | It describes the data set by showing a summary of the data points. |
| 2. Tools for analysis | The tools used are regression analysis and hypothesis tests.
| The tools used are measures of dispersion (range and standard deviation) and central tendency (mean, median, and mode). |
| 3. Uncertainty | There is uncertainty as the behavior of the unknown population is predicted from the results of a known sample. This uncertainty is reflected in the sampling error. | There is no uncertainty as one describes the data points that have been actually measured. |
| 4. Applicability | It is used when each data point of the population cannot be conveniently examined. | It is used when a numerical summary or graphical representation of the data points is required. |
