Gamma Distribution

Published on :

21 Aug, 2024

Blog Author :

Edited by :

Reviewed by :

The gamma distribution is a continuous probability distribution usually employed to model random variables representing durations and waiting times. It contains two parameters, namely, the shape and rate parameters. It is a valuable instrument in analyzing healthcare operations, modeling time-to-failure in reliability analysis, queueing systems, and insurance claim amounts.

The gamma distribution is often applied in several fields, including statistics, physics, economics, and engineering. Furthermore, it offers a flexible and versatile system for modeling continuous random variables related to time and duration. However, the shape parameter in this distribution determines the distribution curve's shape, and the rate parameter controls its scale.

What Is Gamma Distribution?

The gamma distribution is a continuous probability distribution with two parameters: shape and rate. It is a valuable tool for modeling random variables representing durations and waiting times.
The shape parameter defines the distribution curve's shape, and the rate parameter controls its scale. Thus, it is beneficial in processes where the time difference between the events is significant.
It assists in analyzing healthcare operations, modeling time-to-failure in reliability analysis, queueing systems, and insurance claim amounts. Moreover, it is employed in various fields like statistics, physics, economics, and engineering.

Gamma Distribution Explained

The gamma distribution is a continuous probability distribution with two parameters, widely used to model random variables that represent waiting times or durations. The two parameters are the shape parameter which determines the distribution curve's shape, and the rate parameter, which controls the distribution's scale.

The gamma distribution is employed in science to model continuous variables with skewed distributions that are always positive. Additionally, it occurs in processes where the time gap between the events is crucial. Furthermore, it is commonly utilized in the fields of business, statistics, science, and engineering. This distribution is a statistical distribution that is related to the beta distribution.

Properties

The gamma distribution properties are as follows:

For any +ve real number α,

Γ(α) = 0∫∞ ( ya-1e-y dy) , for α > 0.

0∫∞ ya-1 eλy dy = Γ(α)/λa, for λ >0.

Γ(α +1)=α Γ(α)

Γ(m)=(m-1)!, for m = 1,2,3 …;

Γ(½) = √π

Parameters

The gamma distribution parameters are as follows:

Shape Parameter: The shape parameter (α) determines the distribution curve's shape. Higher values of α lead to a more concentrated and peaked distribution. However, lower values result in a more spread-out distribution. When α is an integer, the distribution is known as the Erlang distribution.
Rate Parameter: The rate parameter (β) controls the distribution's scale. Larger values of β lead to a narrower distribution, while smaller values result in a broader distribution.
Threshold Parameter: The threshold parameter controls if the distribution can have negative values. It is usually established as zero, meaning the distribution can accept only positive values.

Formula

The gamma distribution formula is as follows:

f(x) = (β^α * x^(α-1) * e^(-βx)) / Γ(α)

Where,

x is the random variable
α is the shape parameter
β is the scale parameter
e is the base of the natural logarithm, and
Γ(α) is the gamma function.

Graph

The gamma distribution graph is as follows:

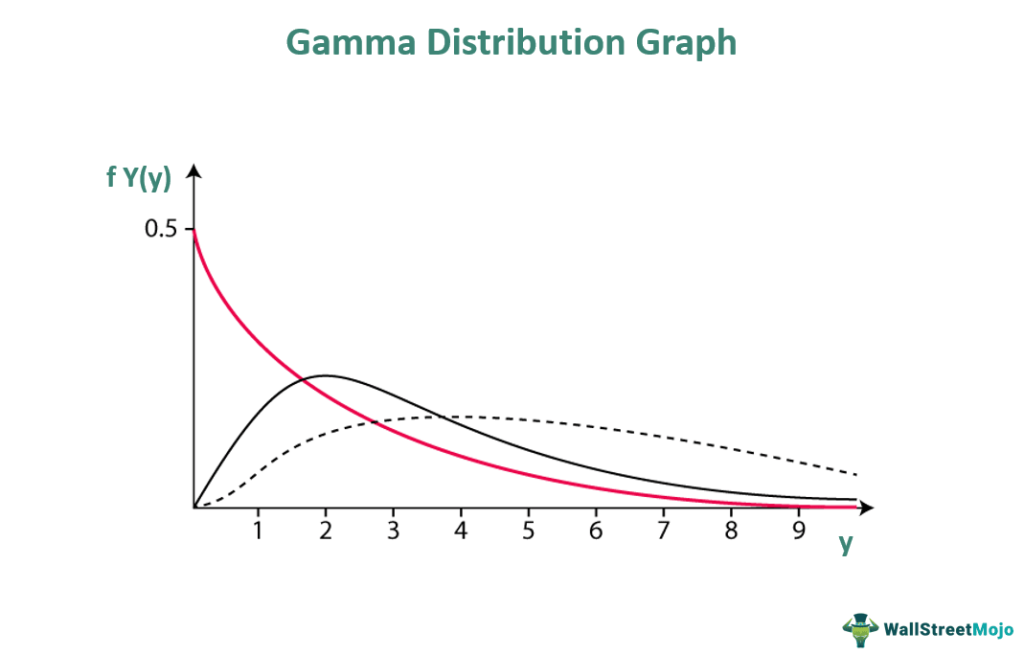
The gamma distribution parameters determine the gamma distribution graph shape. The shape parameter α and the rate parameter β are greater than 1.

However,

When α = 1, it becomes the exponential distribution

When β = 1, it becomes the standard distribution

Applications

The gamma distribution applications are as follows:

Reliability Analysis: This distribution is generally used to model time-to-failure or time-to-repair in reliability analysis. Moreover, it helps estimate components' and systems' reliability and failure rates, which helps in maintenance and decision-making.
Queueing Systems: In queueing theory, it is employed to model inter-arrival times or service times. Additionally, it assists in determining waiting times, system capacity, and resource utilization.
Insurance and Finance: It is applied for modeling insurance claim amounts, capturing the variability in claim sizes, and assisting in risk assessment. Furthermore, it is valuable in financial modeling, like options pricing and calculating asset returns.
Healthcare: This distribution is used in medical research to model survival times, disease progression, and recovery rates. Moreover, it aids in analyzing clinical trial data and assessing treatment outcomes.

Gamma Distribution vs Poisson Distribution vs Exponential Distribution

The differences are as follows:

Gamma Distribution: It is a continuous probability distribution used to model positive continuous random variables. It comprises two parameters: shape (α) and rate (β. It is widely used for modeling waiting times, durations, and time-to-failure data. This distribution is positively skewed and can include a broad range of skewness values. It contains the exponential distribution as a particular case when the shape parameter α equals 1.
Poisson Distribution: The Poisson distribution is a discrete probability distribution used for modeling the number of events that occurs in a fixed interval of time or space. It has one parameter, λ, which represents the average rate of event occurrences. It is used when events occur randomly and independently. It is generally applicable in areas like telecommunications and queuing theory.
Exponential Distribution: It is a continuous probability distribution used to model the time between events occurring in a Poisson process. It has one parameter, λ, which signifies the rate of events occurrences. This memoryless distribution implies that the probability of an event occurring in the future does not depend on how much time has already progressed. It is applicable in reliability analysis, queueing theory, and survival analysis.

Frequently Asked Questions (FAQs)

1. Can gamma distribution be symmetric?

No, this distribution is not symmetric. It is a positively skewed distribution, implying a longer tail on the right side. The shape parameter (α) determines its shape. For α greater than 1, the distribution becomes increasingly skewed to the right. However, when α equals 1, the distribution reduces to the exponential distribution, meaning it is positively skewed. Furthermore, in most cases, the distribution is not symmetric and is skewed to the right.

2. Is gamma distribution an exponential family?

Yes, this distribution is an exponential family of distributions member. An exponential family is a group of probability distributions that can be expressed in a specific mathematical form. This distribution meets the exponential family's criteria because its probability density function (PDF) can be defined as exponential and power functions. Moreover, the shape and rate parameters for this distribution are the natural parameters of the exponential family. Thus, this distribution is a member of the exponential family of distributions.

3. Can gamma distribution be negative?

No, this distribution cannot have negative values. It can have only non-negative values because it models durations, waiting times, or other positive quantities. Furthermore, the probability density function (PDF) for this distribution is non-zero only for values higher than or equal to zero, as the exponential term in the PDF involves the base of the natural logarithm, which is always positive. Thus, this distribution can never be negative.