Game Theory

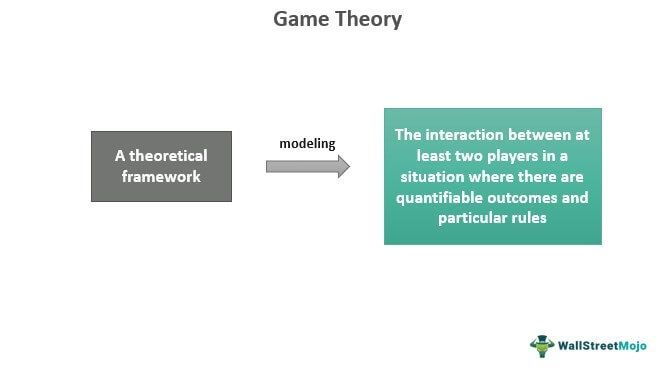
Game theory models the interaction between multiple players in any scenario with specific rules and quantifiable consequences. One can use this theory to analyze situations involving various decisions, limited resources, different outcomes resulting from different choices, and the possibility of competition or collaboration between players.

This mathematical framework primarily serves as an economic tool helping with the fundamental analysis of various industries and the relationship between multiple organizations. Moreover, it can help companies make strategic decisions outside and inside the organization against their peers. There are different types of game theory, like symmetric and asymmetric, cooperative and non-cooperative, simultaneous and sequential, etc.

• Game theory definition refers to a mathematical framework studying strategic decision-making; it aims to predict how multiple players will work in a specific situation.
• Cooperative and non-cooperative, symmetric and asymmetric, simultaneous and sequential are some of the different types of game theory. 
• The theory holds when certain assumptions are true. For example, the number of players in a game setting must be finite, and all participants are rational and intelligent.
• Game theory has multiple limitations. For example, the assumption that participants know about their payoff but not other players’ is unrealistic.

Game theory definition refers to a theoretical framework simplifying social interactions between multiple players competing with each other. It helps to address issues with cooperating or conflicting participants having the ability to make rational choices. The concept aims to find an optimal rational decision in different scenarios, like new product releases, mergers and acquisitions (M&As), etc. A crucial feature of this theory is that a participant’s payoff depends on other participants’ strategies.

An economist named Oskar Morgenstern and mathematician John von Neumann pioneered this theory in the 1940s. One can utilize this concept to identify the most likely consequences whenever a scenario has quantifiable outcomes for multiple players or individuals making strategic decisions in a game context. The game identifies participants’ identities, preferences, available strategies, and how such strategies affect the result. Various assumptions or requirements could be necessary depending on the model.

Despite the various advances, this theory is still in the developing stages. Nevertheless, it has many applications, including politics, evolutionary biology, business, and more.

The different types of game theory are as follows:

#1 - Cooperative And Non-Cooperative

This analysis involves studying how players form binding agreements and allocate payoffs between themselves. In non-cooperative game settings, players cannot get into binding agreements. A non-cooperative game studies how rational individual players decide their strategy to fulfill their objectives.

#2 - Symmetric And Asymmetric

In the case of symmetric games, the payoffs depend on each player’s strategy. Conversely, in asymmetric game settings, the payoffs vary among the players. Hence, the payoff will differ if all players choose an identical strategy.

#3 - Simultaneous And Sequential

A game where players make a decision without knowing other players’ decisions, or all players make their decision simultaneously is a simultaneous game. In sequential games, players are aware of the other players’ decisions, or they take turns to decide.

#4 - Zero-Sum And Non-Zero-Sum

In zero-sum games, a participant’s gains or losses balance other participants’ gains or losses. Contrary to the zero-sum game setting, a player’s gains or losses do not result in other players’ gains or losses in a non-zero-sum game.

#5 - Perfect Information And Imperfect Information

All participants have access to the same information in a perfect information setting. Therefore, they make their decision based on the data. However, in an imperfect information ruleset, the data available to one player is unavailable to other participants.  

Let us look at this game theory example to understand the concept better.

A popular example of this concept is the prisoner's dilemma. Suppose the police arrested two individuals, Jimmy and Ben, for a crime. The prosecutors did not have enough evidence to convict them. Hence, the officials decided to question them in separate chambers to get a confession. They presented these four deals to the arrested individuals.

• If both confess, each of them will get a five-year sentence.
• Jimmy will get three years, while Ben will get nine years if the former confesses and the latter does not.
• Ben will receive a two-year sentence if he confesses, but Jimmy does not.
• If no one confesses, they must serve two years in jail.

Here, the ideal strategy for both is not to confess to the crime. That said, Jimmy and Ben are unaware of each other's decisions. Therefore, both Jimmy and Ben will likely confess to the crime without being sure that the other person will not confess. As a result, both will receive a five-year sentence. Per the Nash Equilibrium, both prisoners will choose the best option individually in such a setting. However, their decisions will turn out to be the worst collectively.

The assumptions of the game theory concept are as follows:

• The number of competitors or players is finite.
• All competitors are rational and intelligent. 
• Every player knows the rules, consequences, and other game-related details.
• Players can opt for different strategies to solve a problem.
• All players in the game have a finite number of courses of action.
• The players aim to minimize losses and maximize gains.
• All players have to make their choice simultaneously to avoid the possibility of a player knowing their competitor’s choice before deciding their course of action.

The limitations of this concept are as follows:

• The assumption that a game’s participants know about their payoffs but not others’ payoffs is impractical.
• The problem-solving methods involving mixed strategies are extremely complicated, specifically in the case of the large payoff matrix.
• One cannot analyze every competitive problem using this concept.

Decision theory studies individuals’ decision-making in scenarios where a person’s choice does not impact others’ decisions, and other individuals’ decisions do not impact the person’s choice. On the other hand, game theory studies decision-making in scenarios where individuals’ choices impact each other’s decisions.

Decision theory asks these questions:

• What does it mean to decide rationally?
• How should one choose when their decision’s consequences are unknown?

Deciding which is the right job or insurance policy to purchase are two examples to help one understand the decisions this theory deals with. That said, the game theory concept applies to every decision with a strategic component. For example, the decisions of oligopolists.

This article has been a guide to What is Game Theory & its definition. We explain its types, assumptions, limitations, example, and comparison with decision theory. You can learn more from the following articles -

• Conflict Theory
• Rational Choice Theory
• Prospect Theory