Download FREE Future Value of Annuity Due Formula In Excel Template and Follow Along!

Future Value of Annuity Due Formula Excel Template.xlsx

Table Of Contents

What is the Future Value of Annuity Due?

Future value of annuity due is value of amount to be received in future where each payment is made at the beginning of each period and the formula for calculating it is the amount of each annuity payment multiplied by rate of interest into number of periods minus one which is divided by rate of interest and whole is multiplied by one plus rate of interest.

Future Value of Annuity Due Formula — *You are free to use this image on your website, templates, etc..* *Please provide us with an attribution link*

Key Takeaways

The Future Value of Annuity Due formula calculates the future worth of a series of equal cash flows received or paid at regular intervals, assuming the payments are made at the beginning of each period.
The formula considers the payment amount, interest rate, and the number of periods to determine the future value of the annuity due.
Time plays a significant role in the future value of an annuity due. The longer the period and the higher the interest rate, the greater the future value.

Future Value of Annuity Due Formula

Publication Date :

04 Jun, 2019

Blog Author :

Edited by :

Reviewed by :

How to Calculate? (Step by Step)

Follow the below steps.

Firstly, figure out the payments that are to be paid in each period. Please keep in mind that the above formula is applicable only in the case of equal periodic payments. It is denoted by P.
Next, figure out the rate of interest to be charged based on the prevalent market rate. It is the rate of interest to be received by the investor if the money is invested in the market. To get an effective rate of interest, divide the annualized rate of interest by the number of periodic payments in a year. It is denoted by r. i.e r = Annualized rate of interest / Number periodic payments in a year
Next, the total number of periods is computed by multiplying the number of periodic payments in a year and the number of years. It is denoted by n. i.e., n = Number of years * Number of periodic payments in a year.
Finally, the future value of an annuity due is calculated based on periodic payment (step 1), the effective rate of interest (step 2), and a number of periods (step 3), as shown above.

Examples

Example #1

Let us take the example of John Doe, who plans to deposit $5,000 at the beginning of each year for the next seven years to save enough money for his daughter’s education. Determine the amount that John Doe will have at the end of seven years. Please note that the ongoing rate of interest in the market is 5%.

fva due example 1.1

Calculate the FV of annuity due for the Periodic Payment using above given information,

fva due example 1.2

FV of Annuity _Due = P * * (1 + r) / r

= $5,000 * * (1 + 5%) / 5%

Future Value of Annuity Due will be -

fva due example 1.3

= $42,745.54 ~ $42,746

Therefore, after seven years John Doe will have $42,746 to spend for his daughter’s education.

Example #2

Let us take another example of Nixon’s plans to accumulate enough money for his MBA. He decides to deposit a monthly payment of $2,000 for the next four years (beginning of each month) so that he is able to gather the required amount of money. As per the education counselor, Nixon will require $100,000 for his MBA. Check if Nixon’s deposits will fund his plans for an MBA, considering the ongoing rate of interest being charged by a bank is 5%.

Future Value of Annuity Due Formula example 2.1

Given,

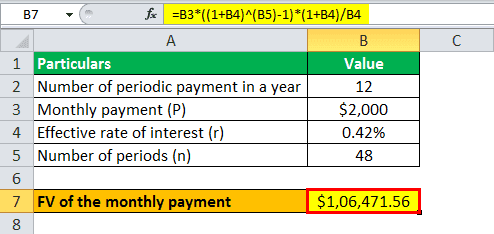
Monthly payment, P = $2,000
Effective rate of interest, r = 5% / 12 = 0.42%
Number of periods, n = 4 * 12 months = 48 months

Calculate the FV of Annuity Due for monthly payment using the above-given information,

Future Value of Annuity Due Formula example 2.2
= $2,000 * * (1 + 0.42%) / 0.42%

Future value of Monthly Payment will be -

Future Value of Annuity Due Formula example 2.3

FV of Annuity _Due = $106,471.56 ~ $106,472

So, with planned deposits, Nixon is expected to have $106,472 which more than the amount ($100,000) required for his MBA.

Relevance and Uses

The future value of an annuity due is another expression of the TVM. The money received today can be invested now that will grow over a period of time. One of its striking applications is in the calculation of the premium payments for a life insurance policy. It also finds application in the calculation of provident fund where the monthly contribution from the salary acts as the periodic payment. The future value of annuity grows based on the stated discount rate. As such, the higher the discount rate, the higher will be the future value of the annuity.