Forward Curve

Last Updated :

Blog Author :

Edited by :

Reviewed by :

Table Of Contents

What Is A Forward Curve?

Forward Curve is a graphical representation of forward contracts using prices based on the underlying index and maturity date. The main aim of this curve is to help analysts and traders predict the trend of these forward contracts in the future.

The forward curve represents the relationship between the prices of forward contracts and their corresponding maturity. Here, the vertical axis represents the forward contracts. Likewise, the horizontal axis states the latter. Thus, on that basis, the direction of the slope is determined. However, the curve faces a limitation of dynamic or changing slopes.

What Is A Forward Curve?

The forward curve is a graphical view of the forward contracts presented using different prices and maturity dates as variables.
The curve's slope can be inverted and normal. A positive relationship defines a normal curve in the upward direction. Likewise, inverted has a downward slope.
In the Contango theory, the curve is above the spot curve. However, in Backwardation theory, it is below the spot curve.
The discount curve involves discounting cash flows of marketable securities to present value. Likewise, spot and swap curves involve spot trades and swap trades with maturities.

Forward Curve Explained

The forward curve or future curve in forward contracts depicts a graph determining the relation between forward contracts and the maturity date. These contracts are based on an underlying market index. Therefore, the forward curve follows the index on the same road. For example, Secured Overnight Financing Rate (SOFR) backs SOFR forward curves.

The forward contracts are deals between parties to trade items on a future date and pre-decided rate. Accumulating various contracts and plotting them will derive the future curve. However, the slope of the curve can vary. If the spot curve rises, the future curve will move above it. However, in certain cases, the reverse can occur. For example, in Contango theory, there is a premium on forward contracts rather than spot prices. As a result, the future curve is above the spot curve. But, in Backwardation theory, the spot curve is above, causing a steep curve.

Based on the relationship, there are two types of forward-curve interest rates. Let us look at them:

Normal curve: A positive relationship exists between the variables (price and duration). Therefore, the slope is upward moving. Plus, it holds net carry costs (for holding the instrument).
Inverted curve: As the name suggests, the direction of this curve is downward-sloping. Plus, it indicates a negative or indirect relationship that holds negative carry costs.

Examples

Let us look at a few examples:

Example #1

In 2015, the London Metal Exchange (LME) started discussions with major bullion trading banks to reinstate end-of-day gold and silver forward or future curves, signaling a potential bigger restructuring in the precious metals market. The future curves, essential for assessing market sentiment, had been discontinued by the LME the previous year due to increased regulatory scrutiny. The exchange started exploring the creation of future curves based on executable forward bids and offers or transactions of daily trades submitted anonymously by banks. This move aligns with regulatory changes aimed at enhancing transparency and reducing vulnerability to manipulation in financial benchmarks.

Example #2

Let's consider an example using oil as a commodity. Mapping forward prices for crude oil delivery at various future dates can illustrate a forward or future curve for crude oil prices based on different delivery dates. Here, the resulting future curve represents the relationship between the prices of forward contracts and their respective maturities.

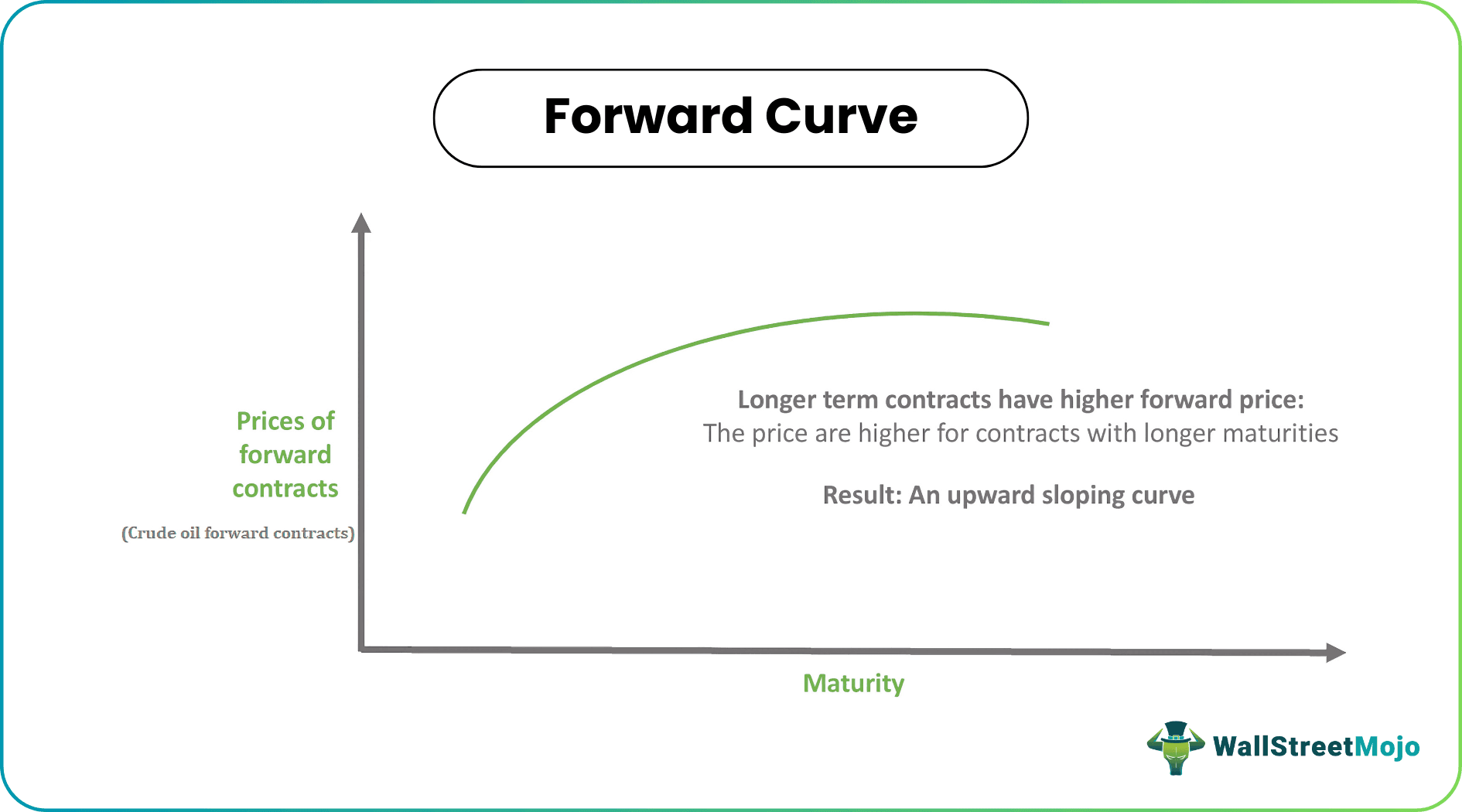
Generally, the prices are higher for contracts with longer maturities, reflecting the cost of carrying and storing oil over time. Hence, the upward-sloping curve is typical in commodity markets and is associated with a normal market condition.

Forward Curve vs Discount Curve

The differences between the two are as follows:

Basis	Forward Curve	Discount Curve
Meaning	It refers to the curve formed from the variable input of the forward contracts.	The discount curve is the slope formed from the discounting of the cash flow stream.
Purpose	To predict the future interest rates for forward contracts and other derivatives trades.	To determine the present value of the future cash flows of an underlying instrument.
Underlying instrument	Forward contracts include market indexes, interest rates, equity swaps, and commodities.	Fixed-income securities like bonds and treasury bills.

Forward Curve vs Spot Curve vs Swap Curve

The differences the between the two are as follows:

Basis	Forward Curve	Spot Curve	Swap Curve
Meaning	It refers to the graphical representation of the forward contracts and their maturity.	The spot curve represents the spot rates and associated maturities on a graph.	The swap curve shows the relationship between fixed coupon rates of market swaps and their maturity dates.
Objective	To estimate the future trends of forward contracts and interest rates.	To determine the present value of the spot trades from the future cash flows.	To calculate the interest rates for the swaps.
Application	Forward contracts	Spot trades	Swap trades
Discounting Factor	Single payment	Spot payments or single cash flows	Here, the interest rates of swaps are used as a discounting factor to derive back to the present cash flows.

Frequently Asked Questions (FAQs)

1. How to build a forward curve?

Following are the steps to build a commodity-like crude forward curve. Let us look at them:
- Collect data about the forward contracts and their maturity.
- Open the spreadsheet and enter the price and maturity date of the contracts.
- Plot the points on the graph and determine the curve.
- Estimating the trend with the help of the slope formed.

2. What is the SONIA forward curve?

SONIA (Sterling Overnight Index) is the market index on which the forward contracts are based. As a result, using the forward curve, analysts can determine the future trends of the curve.

3. Why is the forward curve not a forecast?

Although the curve helps predict future interest rates, many investors and managers use it to determine the levels for a future rate using the current forward contracts. Also, it does not give a guarantee of future rates.