Table Of Contents
What Are Factor Models?
Factor Models refers to the study and assessment of financial models factors (macroeconomic, fundamental, and statistical) to determine the market equilibrium and calculate the required rate of return. Such models associate the return of a security to single or multiple risk factors in a linear model and can be used as alternatives to Modern Portfolio Theory.
Factor models allow entities to study the risk and return associated with a security. The factors that are studied can be basic, technical, macroeconomic, etc. This analysis technique helps investors diversify portfolio based on the profits and losses depicted.
Key Takeaways
- Factor models intricately combine macroeconomic, fundamental, and statistical factors to establish market equilibrium and ascertain requisite rates of return.
- By tethering a security's returns to one or more risk factors within a linear framework, these models offer an alternative avenue to the Modern Portfolio Theory for investment analysis.
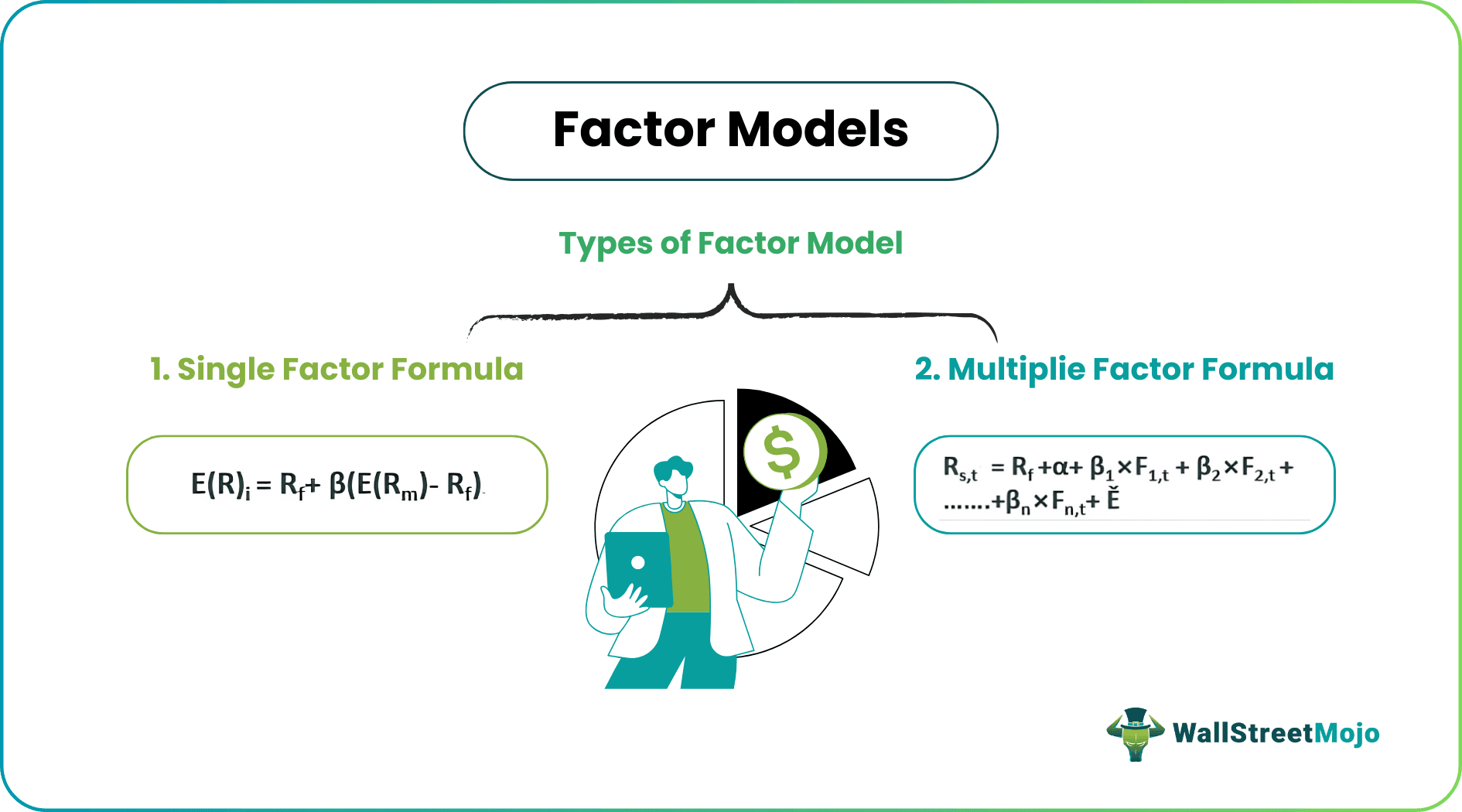
- The realm of factor models is categorized into two principal variants: single-factor and multiple-factor models.
- These frameworks elucidate the interplay of factors affecting asset returns, enabling a deeper understanding of investment dynamics.
Factor Models Explained
Factor models, as the name suggests, are techniques that help assess the risks and returns that a security or financial instrument is supposed to generate or derive. These models take into consideration the factors that commonly influence the financial instruments as well as factors that specifically influence to those instruments only.
Based on the types of factors these models consider, they can be explicit and implicit in nature. The explicit class is the one which depends on the predetermined determinants, which are independent of the data or instrument involved. Such factors are based on the established theories and include determinants, like inflation, economic growth, etc.
On the contrary, the implicit class indicates the model type that depends on the internal input only. Some examples of implicit class of models include factor analysis, component analysis. These analyses not only hep derive factors, but also factor exposures.
These models serve multiple purposes, which make these models one of the most significant risk and reward assessment techniques. Below are some of the functions related to factor models:
- Maximization of the excess return, i.e., Alpha (α) (to be dealt in the later part of this article) of the portfolio;
- Minimization of the volatility of the portfolio, i.e., the Beta (β) of the portfolio;
- Ensure sufficient diversification to cancel out the firm-specific risk.
In short, factor models help investors understand the opportunities, potential, and risks associated with the financial instruments they are willing to invest in. Based on the analysis and assessment of the risk and returns that a security offers, the investors make smarter and wiser investment decisions.
Types
Though there are numerous factor models that exist for the analysts to study, the major ones are single and multiple factor models, which have been discussed in detail below:
- Single Factor
- Multiple Factor
#1 - Single Factor Model
The most common application of this model is the Capital Asset Pricing Model (CAPM).
The CAPM is a model that precisely communicates the relationship between the systematic risk and the expected return of the stocks. It calculates the required return based on the risk measurement. To do this, it relies on a risk multiplier called the Beta coefficient (β).
Formula/structure
E(R)i = Rf+ β(E(Rm)- Rf)
Where E(R)I is the Expected return of investment
- Rf is the Risk-Free Rate of Return defined as a theoretical rate of return with zero risks.
- β is the Beta of the Investment that represents the volatility of the investment as compared to the overall market
- E(Rm) is the Expected return of the market.
- E(Rm)- Rf is the Market Risk Premium.
#2 - Multiple Factor Model
Multiple factor models are adjunctions to single financial models. Arbitrage Pricing Theory is one of its predominant applications.
Formula/structure
Rs,t = Rf +α+ β1×F1,t + β2×F2,t + β3×F3,t+ …….βn×Fn,t+ Ě
Where Rs,t is the Return of security s at Time t
- Rf is the Risk-Free Rate of Return
- α is the Alpha of the security -Alpha is the constant term of the factor model. It represents the excess return of the investment relative to the return of the benchmark index. It is the value by which the investment outperforms the index. Higher the alpha, the better it is for investors
- F1,t, F2,t, F3,t are the factors - Macroeconomic factors like exchange rate, Inflation rate, Foreign Institutional Investors, GDP, etc. Fundamental factors P/E ratio, Market capitalization, etc.
- β1, β2, β3 are the factor loadings. - The factor loadings, also known as component loadings, are coefficients of the factors, as mentioned above. For example, Beta calculation assists the investors to analyze the magnitude by which a stock moves in relation to change in the market.
- Ě represents the error term - The equation contains an error term which is used to give further precision to the calculation. It can sometimes be used to define the security specific news that becomes available to the investors.
Examples
Let us consider the following instance to understand the concept better and check how it works:
Example 1 – Single Factor Model
Consider the following example:
The Beta of a particular stock is 2.The market return is 8%, a Risk-free rate 4%.
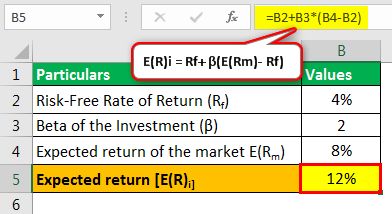
The Expected return as per the above formula would be:
- Expected return E(R)i= 4+2(8-4)
- = 12%
The CAPM is a simple model and is most commonly used in the finance. It is used to calculate the Weighted Average Cost of Capital/ Cost of equity.
But this model is based on a few slightly unreasonable assumptions, such as 'the riskier the investment, the higher the return,' which might not be necessarily true in all the scenarios, an assumption that historical data accurately predicts the future performance of the asset/stocks, etc.
And, what if there are many factors and not just one which determines the rate of return? Hence, we move on to the financial Models and discuss such models in depth.
Example 2 - Multiple Factor Model
Consider the following example:
| Factor | Factor Sensitivity (β) | Risk Premium (F1,t) |
|---|---|---|
| Factor 1 | 0.60 | 0.05 |
| Factor 2 | 0.54 | 0.08 |
Assume the Risk-free Rate of Return to be 4%.
The Return as calculated for the above example is as follows:
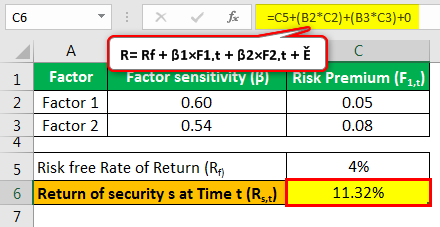
- R= Rf + β1×F1,t + β2×F2,t + Ě
- = 4% + 0.6(5) + 0.54(8)
- = 11.32%
The arbitrage pricing theory being one of the common types of Financial models, is based on the following assumptions:
- A linear factor model can describe asset returns.
- Asset/Firm-specific risk shall possibly be eliminated by diversification.
- No further arbitrage opportunity exists.
Advantages
Factor models help analyze different determinants based on which the reward and risks are assessed, thereby allowing individuals and institutions decide which instruments to invest in for profits and refrain from to avoid losses. This model offers multiple benefits to analysts and users, allowing them to:
- Understand risk exposures of equity, fixed income, and other asset class returns.
- Ensure that an investor’s aggregate portfolio meets his risk appetite and return expectations.
- Build Portfolios that obtain a consistent result or remodel according to the characteristics of a particular index.
- Estimate cost of equity capital for valuation
- Manage Risk and hedge.
Disadvantages
Though there are lots of benefits of using factor models to analyze different factors affecting the rewards and risks associated with an instrument, it is not devoid of flaws. These models have several limitations. Let us have a look at some of them below:
- It is hard to decide how many factors to include in a model.
- Interpretation of the meaning of the factors is subjective.
- Selecting a good set of questions is complicated, and different researchers will choose different sets of questions.
- An improper inquiry might lead to complicated outcomes.


