F-Test in Excel

What is F-Test in Excel?

F-test in excel is a statistical tool that helps us decide whether the variances of two populations having normal distribution are equal or not. F-test is an essential part of the Analysis of Variance (ANOVA) model.

F-test is performed to test a null hypothesisNull Hypothesis Null hypothesis presumes that the sampled data and the population data have no difference or in simple words, it presumes that the claim made by the person on the data or population is the absolute truth and is always right. So, even if a sample is taken from the population, the result received from the study of the sample will come the same as the assumption.read more and gives an independent variableIndependent Variable Independent variable is an object or a time period or a input value, changes to which are used to assess the impact on an output value (i.e. the end objective) that is measured in mathematical or statistical or financial modeling.read more as the result. The sample data used in F-test is not dependent. F-tests can evaluate multiple models simultaneously in a large variety of settings.

How to Enable F-Test in Excel?

The steps to enable F-test in Excel are listed as follows:

Step 1: Enable the “Analysis ToolPak Add-In” in your worksheet to use the F-test. In Excel, click on “File” at the extreme left and go to “Options” given at the end.
Step 2: After clicking on “Options,” select “Add-Ins” on the left side. Select “Excel Add-ins” in the Manage box and click “Go.”
Step 3: In the “Add-Ins” dialog box, click “Analysis Toolpak” and click “Ok.”
Step 4: Now, the “Data Analysis” tool will be added to the right side of the Data tab on the Excel ribbonExcel Ribbon The ribbon is an element of the UI (User Interface) which is seen as a strip that consists of buttons or tabs; it is available at the top of the excel sheet. This option was first introduced in the Microsoft Excel 2007.read more.

How to do F-Test in Excel? (Step-by-Step)

The steps to perform F-test in Excel are listed as follows:

You can download this F-Test Excel Template here – F-Test Excel Template

Step 1: The data used in the F-test analysis is shown in the following image.

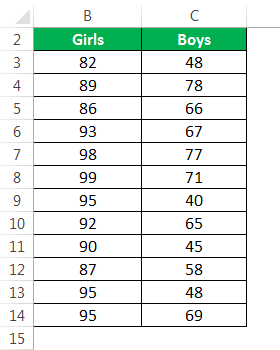
In the Analysis ToolpakAnalysis Toolpak Excel's data analysis toolpak can be used by users to perform data analysis and other important calculations. It can be manually enabled from the addins section of the files tab by clicking on manage addins, and then checking analysis toolpak.read more workbook, you can practice the analysis of the F-test.

Step 2: In the Data tab on the Excel ribbon, click on “Data Analysis.”

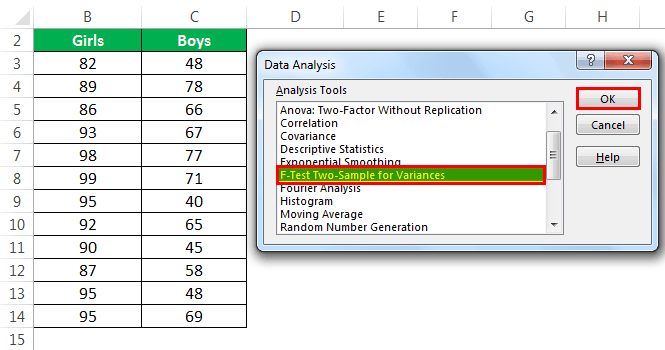
Step 3: After clicking on “Data Analysis,” a dialog box opens. Click on F-test and click “Ok” to enable the function.

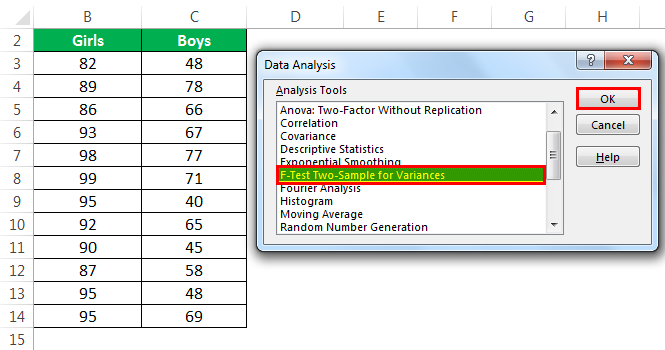
Step 4: Enter the range of variable 1 and variable 2. To do this, select the range of cells B3:B14 for variable 1 and C3:C14 for variable 2.

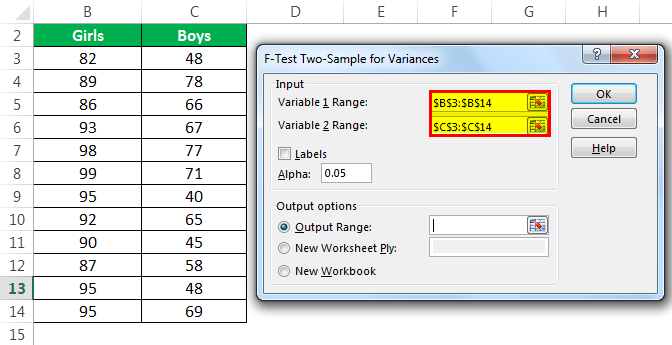
Step 5: Select the “Output Range.”

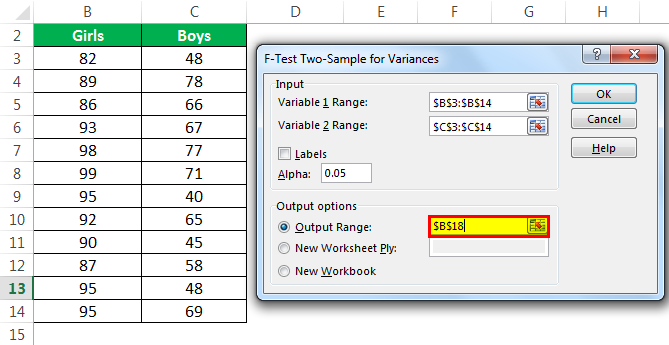
Step 6: Click “Ok” and the analysis of data appears in the selected cell.

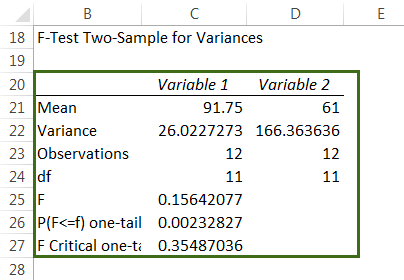
The Working of F-Test

The following points will help learn more about the F-test functionF-test Function F-test formula is used in order to perform the statistical test that helps the person conducting the test in finding that whether the two population sets that are having the normal distribution of the data points of them have the same standard deviation or not.read more:

The F-test is used where we need to figure out whether a critical distinction between the variances of two datasets exists or not.
The null hypothesis is rejected if the variances of the two datasets are unequal and accepted if the variances are equal.
The F-test calculates the probability or the likelihood of variation.
The F-test shows an error if:
1. The number of values of array 1 or array 2 is less than two.
2. The variance of either of the two arrays is equal to zero.
The F-test cannot be processed on a single sample meaning that two datasets are required.
The F-test function ignores the text of sample data and gives numbers as the outcome.

The Examples of F-Test

Some instances where the F-test can be used are listed as follows:

To analyze the quality of lecture of two professors teaching the same subject
To test two samples of bottle gourd in two different experimental conditions
To analyze the scores of two groups in the same field

Frequently Asked Questions

#1 – What is the difference between T-Test and F-Test?

The differences between the two tests are listed as follows:

– A T-testT-test A T-test is a method to identify whether the means of two groups differ from one another significantly. It is an inferential statistics approach that facilitates the hypothesis testing.read more is used to determine whether a significant difference between the means of two datasets exists or not. In contrast, the F-test is used to determine whether the variances of two datasets are equal or not.
– A T-test suggests if a single variable is statistically significant, while F-test suggests if a group of variables are jointly significant.
– The null hypothesis used in a T-test is that the means of two populations are equal. In contrast, the null hypothesis used in F-test is that the variances of two populations are the same.
– The degree of freedom (df) in the T-test is “n-1,” where “n” is the number of sample values. On the other hand, the degree of freedom in the F-test is “n1-1, n2-1,” where “n1” and “n2” are the number of observations in sample 1 and sample 2.

#2 – What is F Statistic in F-Test?

The F statistic or F value is calculated from the data while performing F-test. The F statistic is a ratio of the variances of the two samples. The F statistic is compared with the F critical value to determine whether the null hypothesis may be supported or rejected.

If the F value is greater than the F critical value, the null hypothesis is rejected. F-tests and F statistics are used to test regressions terms, regression models, equality of means, and so on.

#3 – What is the P-value in F-Test?

The P-valueP-value P-Value, or Probability Value, is the deciding factor on the null hypothesis for the probability of an assumed result to be true, being accepted or rejected, & acceptance of an alternative result in case of the assumed results rejection. read more is the probability estimate used in combination with the F statistic to analyze the overall results of the F-test. To accept or reject the null hypothesis, the P-value is compared with the significance level (denoted by alpha).

The P-value is the probability that the results could have happened by chance. For instance, a P-value of 0.01 implies that there is a 1% probability that the results occurred by chance. The individual P values are studied to observe which individual variable is statistically significant.

If the P-value is greater than the significance level, the null hypothesis is accepted. If the P-value is less than the significance level, the null hypothesis is rejected.

The F-test function tests whether two datasets have equal variances or not.
The F-test determines the probability or the likelihood of variation.
The F-test can easily work with multiple models.
To use the F-test function in Excel, enable “Analysis ToolPak Add-In.”
If the variances of the two datasets are unequal, reject the null hypothesis and if the variances are equal, accept the null hypothesis.
The F-test shows an error if the number of values in an array is less than two or the variance of either of the two arrays is equal to zero.

19th/20th September 2020	Saturday - Sunday	9 am IST to 5 pm IST
26th/27th September 2020	Saturday - Sunday	9 am IST to 5 pm IST

F-Test in Excel