F-Test

Last Updated :

Blog Author :

Edited by :

Reviewed by :

Table Of Contents

F-Test Definition

F-Test in statistics is a hypothesis-testing procedure that considers two variances from two samples. The F-Test is used when the difference between two variances needs to be significantly assessed, i.e., when determining whether or not two samples can be taken as representative of the normal population with the same variance.

The F-Test helps to determine the overall significance of the regression. It is useful in various situations, such as when a quality controller wants to determine whether the product's quality is deteriorating over time. In addition, it might be useful for an economist to determine whether income variability varies between two populations.

F-Test Definition

The F-test is a statistical test that evaluates if the variances of the two normal populations are equal.
One can deem the variance ratio of the test insignificant if F OR = F0.5, and one can assume that the values will be from the same group or groups with similar variances.
The null hypothesis is rejected, and the variance ratio is considered significant if F> OR = F0.5.
The F-test vs. t-test: The t-test and the F-test are two separate tests. The T-test compares two populations' means, whereas the other compares two populations' variances.

F-Test in Statistics Explained

F-test in statistics helps to decide whether two populations' variances are equal. This is the variance ratio test because it calculates the ratio of variances. The goal of the test is to determine whether the variance in two populations is equal. It was propounded by British polymath R.A. Fisher and named to honor him. G.W. Snedecor later developed the test.

The following conditions are critical for using the F-test to compare the variances of two populations:

Normality: the populations must have a normal distribution.
Independent and random selection of sample items: the selection of the samples' components should be independent and random.
More than unity: The variance ratio must be one or larger than one; it cannot be less than one. When dividing variance estimates, smaller estimates divide the larger estimates of variances.
The additive property states that the total of different variance components will equal the total variance, i.e., the total variance is the sum of the variance between samples and the variance within samples.

Formula

1. Sample variances: The formula for calculating sample variances is as follows (an online F-test calculator can make it easier):

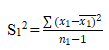
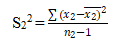
2. Null hypothesis: After the formation of the test, the null hypothesis are either

a) Two samples were from the same group or

(b) The population's variances concerning both samples are equal.

3. To compute the variance ratio, use the formula F = larger estimate divided by a smaller estimate of variance. Regardless of whether S12 or S22, the numerator will always be the larger value.

4. When calculating degrees of freedom, the larger the sample's variance is V1; the smaller variance is V2.

5. Table value of F: the critical value of F is available from the "F-Table" (F-test table) at the determined significance level.

6. Analysis: This involves the comparison of the computed value and the tabulated value. For various levels of significance, there are several F Tables (F-test tables).

(a) The variance ratio is insignificant if F < OR = F0.5. We can assume that the values are from the same group or groups with similar variances.

(b) The null hypothesis is rejected, and the variance ratio is considered significant if F> OR = F0.5.

Calculation Example

Consider the example of the population in a village:

Village	A	B
Sample size	10	12
Mean monthly income	150	140
Sample variance	92	110

Testing the equality of sample variances with a significance level of 5% with the above-given date.

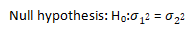
Variance sample for S₁² (sample1) =

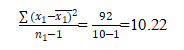
And

Variance sample for S₂²(sample 2) =

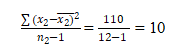
F= S₁²/ S₂^{2 =}10.22/10=1.022

The critical value for v₁(10-1) = 9 and v₂ (12-1) =11 and the table value of F at 5% significance level = 2.90. An online f-test calculator can help you in making the calculations easier.

Interpretation

The F statistic helps to decide whether to accept or reject the null hypothesis. The test results must include an F value and an F critical value. The F value is compared to a particular value known as the F critical value. The value derived from the data is the F statistic, or F value (without the "critical" part). In general, one can reject the null hypothesis if the computed F value for a test is higher than the F critical value.

In the example above, F's computed value (1.022) is less than its table value obtained from the F table (2.90). As a result, one can conclude that the null hypothesis is true and that the variance of the two samples is equal.

Frequently Asked Questions (FAQs)

1. How to do an F-test?

First, the null and alternative hypotheses must be defined, followed by the test statistic. After that, the degrees of freedom should be calculated where n1 and n2 are the sample sizes. Finally, after obtaining the F value, compare the critical value obtained.

2. What is F-test used for?

The F-Test is utilized to determine whether two populations' variances are equal. In addition, it is used to examine the hypothesis that a population's mean values are normally distributed.
It is also utilized to determine whether a suggested regression model accurately predicts the data.

3. What are the t-test and F-test?

The F-test vs. t-test: Any statistical test with an F-distribution for the test statistic under the null hypothesis is known as an F-test. Any statistical hypothesis test known as a "t-test" is one in which the test statistic exhibits a Student's t-distribution under the null hypothesis.

4. Are F-test and ANOVA the same?

Any statistical test employing an f-statistic or f-value is called an "F-test." On the other hand, ANOVA (Analysis of Variance) employs the f-test. This is because the hypothesis has a group of normally distributed populations with a common standard deviation having equal means.