Exponential Excel Function (EXP)

Exponential Excel function in excel is also known as the EXP function in excel which is used to calculate the exponent raised to the power of any number we provide, in this function the exponent is constant and is also known as the base of the natural algorithm, this is an inbuilt function in excel.

Exponential Function in Excel

Excel has an exponential excel function called EXP function, which is categorized as a Math/Trig Function that returns a numeric value, which is equal to e raised to the power of a given number.

Exponential Excel Formula

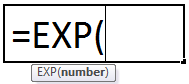
 Exp function in Excel takes only one input, which is required; it is the exponent value raised to base e.

What is e in Mathematics?

The number e is an irrational number, whose value is constant and is approximately equal to 2.7182. This is number is also known as Euler’s Number. The value of the number is calculated by the formula.

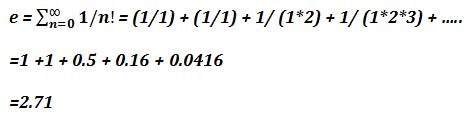
How to Use EXP Function in Excel? (with Examples)

Like LOG function is used when the rate of change in the data increases or decreases quickly; the EXP function in Excel is used when data values rise or fall at increasingly higher rates.

In Excel, while working non-linear trend lines (set of points on an exponential excel function’s graph) or non-linear graphs, the EXP function in Excel is widely used.

An Exponential function in Excel is also used to calculate the growth and decay of bacteria and microorganisms.

Exponential in Excel Example #1

Suppose we have a sample for organic solutions, the lab examiner at time t=0 hours puts one hundred bacteria into the solution in order to determine the suitable growth medium. After 5 hours, the examiner needs to calculate the count of bacteria. The growth rate of the bacteria in the given organic solution is 0.25/hour

Total number of bacteria count at t=0	100
Total time for growth of bacteria (in hrs)	5
Rate of Growth of Bacteria	0.25
Total number of bacteria after 5 hrs	129

For the rate of growth or decay, we have a formula

A=Pe^kt

• Where A is the ending amount
• P is the initial amount
• t is the time of growth or decay
• k is the rate of decay or growth

In this case, A= 500, t = 5 hours, k = 0.25, P=?

So in order to calculate the value of k in Excel, we have to use the exponential in excel and log function.

P = A/e^kt

Therefore, P = A/EXP(k*t)

In Excel, the formula will be

=ROUND(D3+D3/(EXP(G3*F3)),0)

After 5 hours, the total number of bacteria in the given organic solution will be near around 129 in a count.

Exponential in Excel Example #2

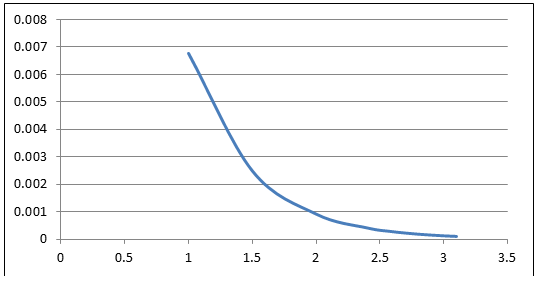
We have a function f(x) that is an exponential function in excel given as y = ae^-2x where ‘a’ is a constant, and for the given value of x, we need to find the values of y and plot the 2D exponential functions graph.

x	1	1.5	2	2.4	2.6	2.7	2.8	2.9	3	3.1
y	?	?	?	?	?	?	?	?	?	?

The value of a is 0.05

To compute the value of y, we will use the EXP function in excel so the exponential formula will be

=a* EXP(-2*x)

Applying the exponential formula with the relative referenceRelative ReferenceIn Excel, relative references are a type of cell reference that changes when the same formula is copied to different cells or worksheets. Let's say we have =B1+C1 in cell A1, and we copy this formula to cell B2 and it becomes C2+D2.read more, we have

=$B$5*EXP(-2*B2

Applying the same exponential formula to other cells, we have

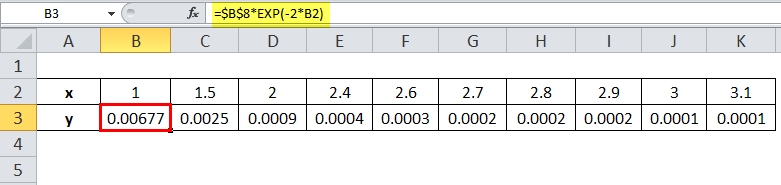
Plotting the graph of the exponential function on the x-y axis, we have the following graph for the above-given function and values

Exponential in Excel Example #3

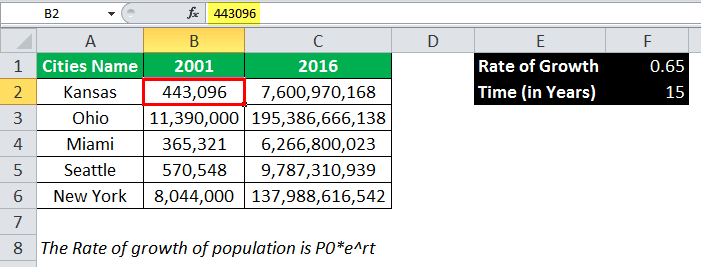
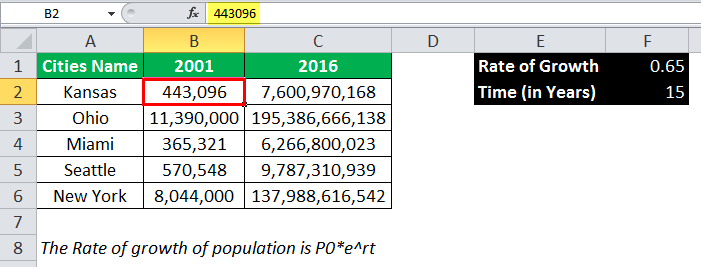
Suppose we have the population data of 5 different cities given for the year 2001, and the rate of growth of the population in the given cities for 15 years was approximately 0.65%. We need to calculate the latest population of the given cities after 15 years.

For the rate of growth, we have the formula,

P = P₀*e^rt

Where P is the latest population (which we will calculate in this case)

P₀ is the initial population

r is the rate of growth

t is the time

Here, in this case, we have to calculate P for five different cities with the given rate of growth of 0.65

So in order to calculate the rate of growth of the population, we will use the above population growth formula

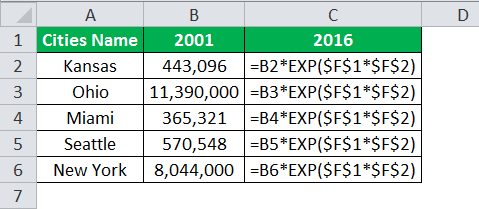
In Excel to calculate the Exponential power, we will further use the Exponential Function in Excel, so the exponential formula will be

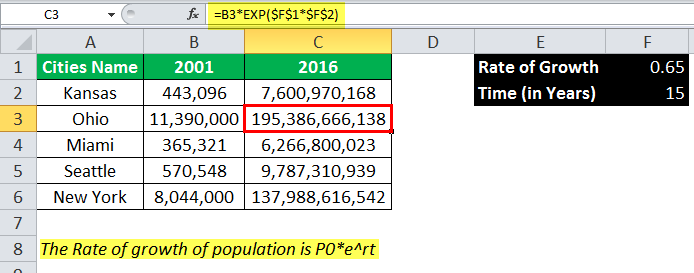
=B2*EXP($F$1*$F$2)

Applying the same exponential formula in reference to other cities, we have

Output:

The Exponential Function in Excel is also used for also calculating the probability distribution in the statisticsStatisticsStatistics is the science behind identifying, collecting, organizing and summarizing, analyzing, interpreting, and finally, presenting such data, either qualitative or quantitative, which helps make better and effective decisions with relevance.read more, also known as the exponential probability distribution. The exponential distributionExponential DistributionExponential distribution refers to the continuous and constant probability distribution which is actually used to model the time period that a person needs to wait before the given event happens. This distribution is a continuous counterpart of a geometric distribution that is instead distinct.read more deals with the amount of time for a specific event to occur.

The Exponential function in Excel has also been used in the regressions linear modeling in the statistics.

Things to Remember About Exponential Function (EXP) in Excel

The Exponential function in Excel is often used with the Log function; for example, in case, if we want to find the rate of growth or decay, in that case, we will use the EXP and the LOG function together.

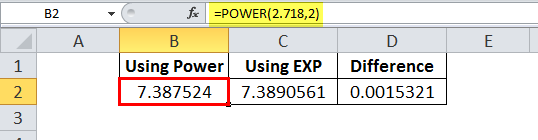
We can also use the POWER function in place of the Exponential function in Excel, but the only difference is the measurement precision.  While using the POWER function, we can provide the of e as 2.71 or maybe up to 3-4 decimal places; however, the EXP function in excel, in general, takes the value of e to 9 decimal places.

So, if we are calculating an Exponential in excel Series, of dealing with non-linear exponential functions graph in which we have the Exponential value, it is better to use the EXP function in excel instead of the POWER functionPOWER FunctionPOWER function calculates the power of a given number or base. To use this function you can use the keyword =POWER( in a cell and provide two arguments one as number and another as power.read more.

EXP function in excel always takes the numeric value as an input; if we provide any other input other than the numeric value, it generates #NAME? Error.

While dealing with the complex Exponents, for example, =EXP(-(2.2/9.58)^2), one should be careful with the brackets, if we mess up with the brackets, the output may differ from the actual output, so it should be =EXP(-((2,2/9,58)^2))

Recommended Articles

This has been a guide to Exponential Function in Excel. Here we discuss the Exponential Formula and how to use EXP in Excel along with Exponential Function examples and downloadable excel templates. You may also look at these useful functions in excel –

• Exponential Smoothing in Excel
• MID in Excel
• Concatenate Function in Excel
• Strikethrough in Excel